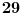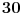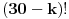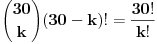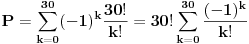[ Bude83 @ 04.07.2005. 12:56 ] @
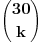
| Spremajući ispit iz diskretne matematike naišo sam na zadatak za cije rjesavanje mi je potrebna pomoc. Zadatak glasi: Koliko se tajnih kodiranja može napraviti tako da svakom slovu abecede pridružimo (jedinstveno) neko drugo slovo. (Abeceda ima 30 slova) Ja sam pokusao da radim na sledeci nacin ali ne znam da li je i koliko ovo ispravno. Pođimo od slova A. Prilikom njegovog kodiranja mozemo da ga zamjenimo sa 29 slova. Uzmimo sada slovo B. Njega mozemo zamjeniti sa 28 jer smo jedno slovo uzeli za kodiranje slova A. C - 27, D - 26,... Pa po mome ispada da je riješenje svega ovoga: Riješenje: 29!=884176199373970194543616000000 |