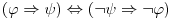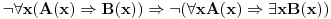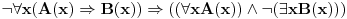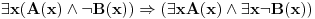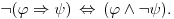[ bayone81 @ 05.07.2005. 17:06 ] @
|
| Cao filozofi i matematicari. Imam jedan problem. Radi se o jednom tipu zadataka mat. logike, koji ne mogu da skapiram.
Ex - postoji x
Vx - svaki x
P = [ExA(x) --> VxB(x)] --> Vx(A(x) --> B(x)).
Da li je ova formula validna, zadovoljavajuca ili kontradiktorna? Ako je ispravna(validna), dokazati u proizvoljnom formalnom sistemu,ako je kontradiktorna dokazati formulu NOT P, ako je zadovoljavajuca(a da nije validna) dati jednu interpretaciju u kojoj je P tacna i jednu u kojoj je P netacna.
hvala unapred |
[ KPYU @ 08.07.2005. 00:33 ] @
Formula je validna.
Prvo koristim zakon kontrapozicije
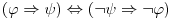
tj tvrđenje važi akko
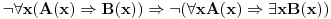
Pošto je

to je
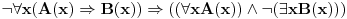
Takođe znamo da

kao i

te dobijamo
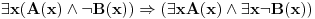
A ovo je valjano.
[ Jorda @ 09.07.2005. 16:46 ] @
Samo jedno pitanje za KPYU:

Zar se u ovom zapisu implikacije ne koristi "ILI" umesto "I" ?
[Ovu poruku je menjao Jorda dana 09.07.2005. u 17:46 GMT+1][ Nedeljko @ 09.07.2005. 18:35 ] @
Mislilo se na
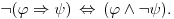
[ Jorda @ 09.07.2005. 22:52 ] @
Naravno, bila je negacija ispred, samo kad je navodio pravilo pogresio je
Pozdrav!
[ Tijana @ 12.12.2007. 11:51 ] @
Moze li neko da mi malo pojasni kako se rade ovakvi zadaci?
1.Na skupu Ρ, svih ravni u prostoru definisana je relacija ρ sa: α ρ β α i β su ortogonalne. Naci najmanju relaciju ekvivalencije koja sadrzi relaciju ρ.
2.Naci najmanju relaciju ekvivalencije koja sadrzi relaciju deljivosti na skupu N\{0}.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.