Zadatak se svodi na pronalaženje broja zapisa broja u osnovi 2 ali sa dopuštenjem da cifre budu od 0 do 3.
Ako prvo pođemo od regularnog zapisa u osnovi 2, dakle samo preko 0 i 1, onda premeštanjem jedinica "udesno" one uvećavaju cifru desno od sebe za 2.Uzastopnim prebacivanjem po jedne cifre (ili njenog dela), pazeći pri tom da ne premašimo gornju granicu za cifre, možemo dobiti sve one neobične zapise.
Da bi bilo jasnije na šta mislim, evo nekih primera:

5= 101= 021= 013
6= 110= 030= 102= 022
7= 111= 031= 103= 023

12= 1100=0300=1020=0220=1012=0212=0132
13= 1101=0301=1021=0221=1013=0213=0133

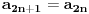
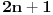
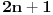
Dakle, ako sa označimo broj zapisa broja , onda je jasno da mora važiti , jer se iz svakog zapisa za , uvećanjem poslednje cifre za 1, dobija zapis za , ( jasno je da su poslednje cifre u bilo kom zapisu za ili 0 ili 2, pa njihovo uvećanje za jedan daje korektnu cifru) i obrnuto, na ekvivalentan način dobijamo da svaki zapis za proizvodi jedan zapis za .

Dakle, dovoljno je pronaći .
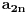
Ako pođemo od regularnog binarnog zapisa vidimo da je zapis broja početni deo zapisa broja .
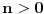
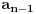
Pošto je paran, to je poslednja cifra 0, a početni deo je zapis broja . Dakle, zapisa broja , koji se završavaju sa 0, ima tačno onoliko koliko i zapisa broja , pa ako je onda je u nekom od zapisa broja poslednja cifra barem 1, pa postoje i zapisi broja koji se završavaju sa 2, jer možemo prebaciti jednu jedinicu iz poslednje cifre zapisa broja , sada broj postaje broj a njegovih zapisa ima , pa smo došli do formule:

.
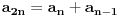
Jasno je da važi .

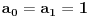
Lako je proveriti da je

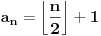
Nadam se da je ovo dovoljno za nagradu


<sub>[Ovu poruku je menjao uranium dana 09.07.2005. u 02:15 GMT+1]

[Ovu poruku je menjao uranium dana 09.07.2005. u 02:43 GMT+1]

[Ovu poruku je menjao uranium dana 09.07.2005. u 02:56 GMT+1]</sub>

Uh bre, iskomplikovao si ga samo tako, ali bitno je da je tačno. Zaslužio si svoju nagradu :)

Rešenje 1: (zvanično rešenje)

Neka je jedan polinom koji zadovoljava uslove zadatka (za neko odabrano ). Definišimo funkciju koja preslikava na tako da su koeficijenti polinom ostaci koeficijenata polinoma pri deljenju sa . Posmatrajmo šta se dešava pri ovakvom preslikavanju: svaki koeficijent polinoma ili umanjujemo za ili ostavljamo isti, na osnovu čega sledi da se vrednost (što je jednako ) može smanjiti za broj oblika gde je zbir nekoliko stepena dvojke (i to tačno onih stepena čije koeficijente smo smanjivali). Pošto se svaki prirodan broj može jednoznačno predstaviti kao zbir stepena dvojki (to je ekvivalentno njegovom binarnom zapisu) sledi da je posmatrana funkcija zapravo bijekcija. Moguće vrednosti polinoma su (pozitivni brojevi) kojih očigledno ima pa toliko ima i polinoma .

Rešenje 2: (profesorovo rešenje)

Neka je . Primetimo da su zapravo svi mogući zapisi broja . Za neparno broj očigledno iznosi ili , a za parno je jednako ili , pa možemo sastaviti sledeću rekurentnu relaciju:



Isprobavanjem za male vrednosti možemo pretpostaviti da je rešenje , za koje dokazujemo indukcijom da važi napisana rekurentna formula (taj deo preskačem ovde pošto nije težak a nema mnogo veze sa samim zadatkom, sve je dalje stvar tehnike).

Rešenje 3: (moje rešenje)

Neka je . To možemo zapisati i kao . Pošto koeficijenti pripadaju skupu ovo u zagradama možemo posmatrati kao prirodne brojeve zapisane u osnovi , pa je broj načina da se predstavi u traženom obliku jednak broju celih nenegativnih rešenja jednačine , odnosno traženi broj je .

Eto, jesi li zadovoljan nagradom? :)

Jesam

Moje rešenje je najbliže rešenju pod 2.
A ono treće je stvarno prelepo

Vidim naucio si funkcije generatrisa :-)

@cassey:
To mi je bio maturski (ako hoćeš mogu ti poslati) :)