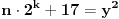
Primetimo prvo da ako za neko važi , onda je neparno (jer je ).
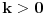
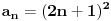
Posmatrajmo sada niz , za
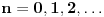
Pogledajmo razliku .
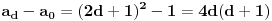
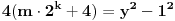
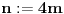
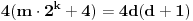
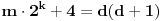
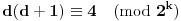
Traženu jednačinu možemo zapisati kao , gde smo uzeli da je . Pošto je desna strana jednaka razlici dva neparna kvadrata, dobijamo da za neko važi , tj. , dakle dovoljno je dokazati da jednačina ima rešenja po .

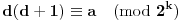
Dokazaćemo da jednačina ima rešenja za svako .

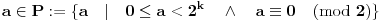
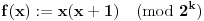
Neka je i neka je . Pokazaćemo da je .

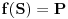
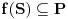
Pre svega, jasno je da važi , jer je proizvod jednog parnog i jednog neparnog broja.

Dokažimo još i injektivnost f-je na skupu .

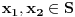
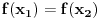
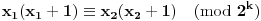
Neka za neke važi , tj. , odnosno .

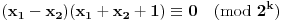
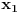
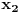
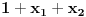
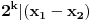
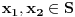
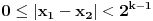
Ako su i iste parnosti, onda je broj neparan, pa mora biti da , ali pošto je , važi procena , pa mora biti .

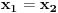
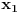
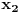
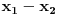
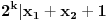
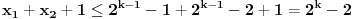
Ako i nisu iste parnosti, onda je neparan, pa mora biti , a to je nemoguće zbog procene (različita parnost je uzeta u obzir u ovoj proceni).

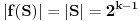
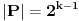
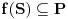
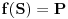
Pošto je injektivna to je , pa iz i sledi a time i samo tvrđenje.

Možemo primetiti još i to da je sada lako pokazati da za dato postoji beskonačno mnogo prirodnih za koje važi tvrđenje.

Hvala ti puno, pogledacu resenje detaljnije ovih dana.