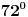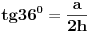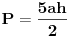[ Nikola Krajačić @ 10.07.2005. 14:10 ] @
| Pozdrav! Ovako, zadan je pravilni peterokut s dijagonalom d=11. Kolika je njegova površina? E, sad, ono do čega sam ja došao jest da je kut alfa=72°, kut beta=108°. Ono što mene zanima jest, kad imam karakteristični torkut tog peterokuta, on se sastoji od baze "a" i dva kraka "r", right? E, mene zanima da li je taj krak "r" možda polovina dijagonale? To mi je jedino logično objašnjenje, jer ne vidim nikakvu drugu povezanost s dijagonalom... |