Pa, možemo da iskoristimo tvrđenje (oslabljeni
Bertrandov postulat), da za svako prirodno

, postoji prosto

za koje važi
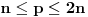
.
Pošto je za
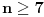
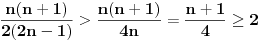
dobijamo da za
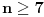
, jednačina nema rešenja, jer će postojati prosto

koje deli desnu a ne deli levu stranu.
Za
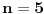
, desna strana je deljiva sa 11, a leva nije.
Za
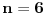
, desna strana je deljiva sa 13, a leva nije.
Sada se lako proveri da je skup rešenja
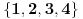
.
Nisam uspeo da ga sabijem u jednoj liniji, verovatno mi je ona procena pregruba
