[ Bojan Basic @ 12.08.2005. 19:56 ] @
|
[ neor @ 13.08.2005. 12:47 ] @
Mislim da imam jedno resenje.
Definisemo pomocne funkcije Fb(x) za b=2,3,... Fb(x) = { 0 za x=0; 1 za b2k <= x < b2k+1, k ceo broj; -1 za b2k+1 <= x < b2k, k iz Z } Sada za svako n funkciju f(x) definisemo preko pomocnih funkcija Fb: f(x) = F2(x) +...+ Fn(x) Ovako konstruisana funkcija zadovoljava uslove zadatka. Izgleda suvise jednostavno pa se bojim da sam negde zabrljao. [Ovu poruku je menjao neor dana 13.08.2005. u 13:50 GMT+1] [ Bojan Basic @ 13.08.2005. 14:15 ] @
Zanimljivo deluje, ali bojim se da nije dobro. Nisi rekao kako definišeš tvoje pomoćne funkcije za negativne brojeve ali to je manje bitno jer ih možeš definisati isto kao i pozitivne - ako valja jedna strana valjaće i druga. Međutim, ovde imaš veću grešku, konkretno recimo za
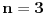 ako ubaciš ako ubaciš 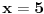 dobiješ da je dobiješ da je 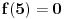 što se ne slaže sa uslovom što se ne slaže sa uslovom 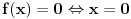 . .U svakom slučaju jako mi se sviđa ideja i sigurno može da se iskoristi nekom drugom prilikom. [Ovu poruku je menjao Bojan Basic dana 26.08.2005. u 11:09 GMT+1] [ neor @ 13.08.2005. 15:02 ] @
Da, nisam pazio na taj prvi uslov to da ne moze da bude nula nigde osim u nuli :(
[ malada @ 26.08.2005. 02:39 ] @
Ja sam malo razmisljao ali uspjeo sam da nadjem rijesenje samo za parno n.
f(X)=sin((10x/pi))+2 za x element [2k,2k+1) f(X)=sin((10x/pi))-2 za x element [2k+1,2k+2) Nije nesto ali... [ StratOS @ 11.09.2005. 10:53 ] @
Malo na brzinu ako je f(x) polinom
ako je f(0)=0 onda je f'(n*x)=n*f'(x)=0 f''(n*x)=f''(n)*f''(x) f''(n)=0 [Ovu poruku je menjao StratOS dana 11.09.2005. u 12:05 GMT+1] [ Bojan Basic @ 02.12.2005. 13:49 ] @
[ malada @ 22.01.2006. 12:20 ] @
E pazi imam jednu ideju, ovo gore nevalja nista, radi za x=1 ili tako nesto. Ideja da funkciju zadam (za dato parno n) sa f(ix)=(-1)^i*(x/i) ali je problem sto funkcija nije jednoznacna, ako bi ovo uspio da premostim onda bi lako moglo da se uopsti i za neparno n.
[ Bojan Basic @ 22.01.2006. 12:51 ] @
Nije mi jasan cilj koji želiš da postigneš. Možeš li da na primeru pokažeš zašto bi u tvojoj konstrukciji važili uslovi zadatka? Nije bitno što funkcija nije jednoznačno određena, odaberi vrednosti kako god ti hoćeš samo da vidim na šta ciljaš, pa posle možemo dorađivati.
[ malada @ 22.01.2006. 12:57 ] @
Pa nesto tipa x=3 f(3)+f(2*3)+f(3*3)+...+f(n*3)=0, ali vidim da mnooogo nije jednoznacna.
[ Bojan Basic @ 22.01.2006. 13:02 ] @
[ malada @ 22.01.2006. 13:21 ] @
Jesi li probao da se zajebavas sa redovima?
Ja sam pokusao da napravim nesto od (valjda) ojlerove funkcije (njene male modifikacije) f(x)=1 ako je x racionalan a -1 ako je iracionalan ali izgleda da neide tako. [ Farenhajt @ 23.01.2006. 12:01 ] @
Mene ovo neodoljivo podseća na jedan zadatak koji je uranium rešio (ne mogu sad da nađem topic), a tiče se funkcije na pravilnim poligonima. Ovde su poligoni, doduše, degenerisani, ali mislim da je princip vrlo sličan - tamo je dobijen rezultat da funkcija mora biti identički jednaka nuli, te se uslov
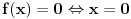 ne može zadovoljiti. ne može zadovoljiti.Uraniume, ako sam na dobrom tragu, preuzmi. [ srki @ 23.01.2006. 12:34 ] @
Ajde na brzinu da napisem sta mi pada na pamet. Mislim da funkcija postoji ali ne mogu tacno da nadjem kako glasi jer dobijem jednacinu cije resenje ne mozemo predstaviti elementarnim funkcijama nego ga mozemo numericki naci ako zelimo odredjenu preciznost. Verovatno je svima prvo palo na pamet da se iskoristi stepenovanje kompleksnog broja jer ako je x=1 onda cemo imati f(1)+f(2)+...+f(n)=0 a ako je funkcija ((n-ti koren iz 1) na x) [neka moderator ubaci tex ako ga ne mrzi ili cu ja sutra] onda cemo u zbiru imati nula. Naravno posto se trazi preslikavanje iz R u R onda mozemo uzeti samo Realni ili imaginarni deo te funkcije. Sada ostaje problem sto mi nemamo f(1)+f(2)+..+f(n)=0 vec f(x)+f(2x) itd...To mozemo resiti tako sto cemo prvo uzeti logaritam od toga pa onda neki kompleksni broj stepenovati sa tim brojem. Znaci f(x)=Re{C^(logx)} ili f(x)=Im{C^(logx)}.
Zasto tako? Zato sto kada 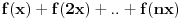 razvijemo onda dobijemo Re{(C^(logX))*(C^(log1)+C^(log2)+..+C^(logn))}. Nadam se da nisam negde pogresio do ovde. E sada samo treba naci C tako da bude (C^log1+C^log2+..+C^logn)=0 sto je moguce uraditi zbog [Izgleda da ovo nije tacno, nesto mi palo na pamet ali sam izgleda pogresio. Mozda mogu da se iskoriste neka svojstva analitickih funkcija ali nemam sad vremena da procesljavam teoreme]. E sada nam ostaje jos samo da resimo problem kada je f(x)=0 ali nisam dalje razmisljao o tome. Mozda da stavimo neku diskretnu vrednost (npr. 1) pa onda za ostale f(2x), f(3x) itd da stavimo neke druge vrednosti. Bojane, je l' sam na dobrom putu ili sam totalno omasio? razvijemo onda dobijemo Re{(C^(logX))*(C^(log1)+C^(log2)+..+C^(logn))}. Nadam se da nisam negde pogresio do ovde. E sada samo treba naci C tako da bude (C^log1+C^log2+..+C^logn)=0 sto je moguce uraditi zbog [Izgleda da ovo nije tacno, nesto mi palo na pamet ali sam izgleda pogresio. Mozda mogu da se iskoriste neka svojstva analitickih funkcija ali nemam sad vremena da procesljavam teoreme]. E sada nam ostaje jos samo da resimo problem kada je f(x)=0 ali nisam dalje razmisljao o tome. Mozda da stavimo neku diskretnu vrednost (npr. 1) pa onda za ostale f(2x), f(3x) itd da stavimo neke druge vrednosti. Bojane, je l' sam na dobrom putu ili sam totalno omasio?[Ovu poruku je menjao srki dana 23.01.2006. u 14:00 GMT+1] [ uranium @ 23.01.2006. 13:25 ] @
Citat: Farenhajt: Mene ovo neodoljivo podseća na jedan zadatak koji je uranium rešio (ne mogu sad da nađem topic), a tiče se funkcije na pravilnim poligonima. Ovde su poligoni, doduše, degenerisani, ali mislim da je princip vrlo sličan - tamo je dobijen rezultat da funkcija mora biti identički jednaka nuli, te se uslov 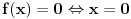 ne može zadovoljiti. ne može zadovoljiti.Uraniume, ako sam na dobrom tragu, preuzmi. Da, na odličnom si tragu Pošto trenutno nemam vremena, napisaću samo osnovnu ideju: Neka je 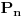 skup prvih skup prvih 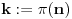 prostih brojeva. Definišemo relaciju ekvivalencije na skupu prostih brojeva. Definišemo relaciju ekvivalencije na skupu 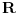 na sledeći način: na sledeći način: 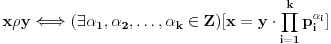 . Dovoljno je da definišemo funkciju na svakoj od klasa ekvivalencije. . Dovoljno je da definišemo funkciju na svakoj od klasa ekvivalencije.Sada uzmimo  dimenzionalni koordinatni sistem i svakoj osi pridružimo jedan od onih dimenzionalni koordinatni sistem i svakoj osi pridružimo jedan od onih  prostih brojeva (svakoj celobrojnoj tački prostih brojeva (svakoj celobrojnoj tački 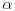 na osi na osi  pridružimo broj pridružimo broj 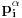 ). ).Neka je  proizvoljna netrivijalna klasa ekvivalencije relacije proizvoljna netrivijalna klasa ekvivalencije relacije  i neka je i neka je 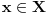 njen bilo koji predstavnik. Uočimo politop sa temenima u tačkama skupa njen bilo koji predstavnik. Uočimo politop sa temenima u tačkama skupa 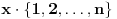 odaberimo vrednosti f-je u tim tačkama proizvoljno ali tako da važi uslov zadatka. Sada možemo ovaj politop da transliramo paralelno svakoj od osa (što se u stvari svodi na množenje/deljenje odgovarajućim prostim brojevima) i da vršimo dalje definisanje f-je, ali ovde stvari postaju suviše tehničke, pa ću to da objasnim detaljno večeras. odaberimo vrednosti f-je u tim tačkama proizvoljno ali tako da važi uslov zadatka. Sada možemo ovaj politop da transliramo paralelno svakoj od osa (što se u stvari svodi na množenje/deljenje odgovarajućim prostim brojevima) i da vršimo dalje definisanje f-je, ali ovde stvari postaju suviše tehničke, pa ću to da objasnim detaljno večeras.Inače, znam za jedno neverovatno rešenje preko Hamel-ove baze, ali njega nisam ja smislio [Ovu poruku je menjao uranium dana 23.01.2006. u 14:27 GMT+1] [ Farenhajt @ 23.01.2006. 13:34 ] @
Mada ni Srkijeva ideja ne izgleda loše. Doduše, možda se može pojednostaviti, ako se stavi da je
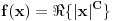 gde gde  zadovoljava uslov zadovoljava uslov 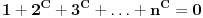 . Samo još da se dokaže da takvo . Samo još da se dokaže da takvo  postoji, i da postoji, i da 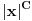 ne postaje čisto imaginaran broj ni za jedno ne postaje čisto imaginaran broj ni za jedno 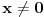 . (Ovo drugo mi deluje kao znatno veći kamen spoticanja.) . (Ovo drugo mi deluje kao znatno veći kamen spoticanja.)[Ovu poruku je menjao Farenhajt dana 23.01.2006. u 14:47 GMT+1] [ uranium @ 24.01.2006. 13:28 ] @
Evo, da dopunim onaj moj prethodni post.
Prvo, obrazloženje zašto uopšte posmatramo onu relaciju  i politope. Izaberimo bilo koje i politope. Izaberimo bilo koje 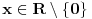 . Posmatrajmo sada sve skupove od po . Posmatrajmo sada sve skupove od po  brojeva na koje će definisanje broja brojeva na koje će definisanje broja  imati uticaja: imati uticaja: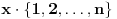 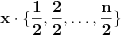  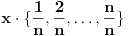 . .Jasno je da se svaki od ovih skupova može dobiti multiplikativnom translacijom bilo kog drugog navedenog skupa. Ali sada moramo da definišemo f-ju i u svim preostalim navedenim tačkama, što nas opet vraća na generisanje novih  -torki (koje se opet mogu dobiti translacijom ovih postojećih). A za samu translaciju dovoljno je da množimo (odnosno delimo) samo sa prostim brojevima ne većim od -torki (koje se opet mogu dobiti translacijom ovih postojećih). A za samu translaciju dovoljno je da množimo (odnosno delimo) samo sa prostim brojevima ne većim od  . .Neka je  prost broj i neka je kao i obično prost broj i neka je kao i obično 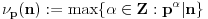 f-ja definisana na f-ja definisana na 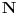 . .Ako uzmemo kao u mom prethodnom postu da je 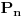 skup prvih skup prvih 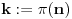 prostih brojeva, onda definišimo multiplikativnu grupu generisanu skupom prostih brojeva, onda definišimo multiplikativnu grupu generisanu skupom 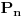 tj. neka je tj. neka je 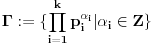 . .Sada primetimo da prilikom svake translacije politopa 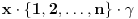 (pri čemu je (pri čemu je 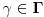 ) "za" broj ) "za" broj 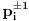 dobijamo novi politop koji će imati zajedničkih temena sa prethodnim, ali će (a to je bitnije) imati i barem jedno novo teme. Evo barem jednog novog temena: neka je dobijamo novi politop koji će imati zajedničkih temena sa prethodnim, ali će (a to je bitnije) imati i barem jedno novo teme. Evo barem jednog novog temena: neka je 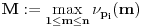 neka je neka je 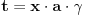 teme politopa kod koga je teme politopa kod koga je 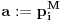 ako je translirano za ako je translirano za 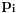 odnosno odnosno 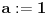 ako se radi o translaciji za ako se radi o translaciji za 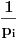 . Lako je videti da za celo . Lako je videti da za celo 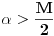 translati za translati za 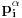 i i 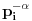 nemaju zajedničkih temena. A u slučaju kada je nemaju zajedničkih temena. A u slučaju kada je 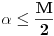 onda pomenuti translati imaju barem po jedno teme koje se nije "pojavilo" ni u jednom translatu za onda pomenuti translati imaju barem po jedno teme koje se nije "pojavilo" ni u jednom translatu za 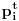 gde je gde je 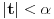 i i 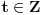 . .Dakle, nakon inicijalnog definisanja f-je u temenima osnovnog politopa, svaka njegova elementarna translacija imaće neprazan skup novih temena pa ćemo moći da f-ju dodefinišemo u njima tako da f-ja zadovolji traženi uslov na translatu. Najzad smo spremni da krenemo na glavni deo. Potreban nam je neki algoritam koji će nam translacijom "prošetati" osnovni politop 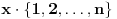 po svim preostalim politopima (sa temenima iz iste klase ekvivalencije) ali tako da preko svakog pređemo tačno jednom. po svim preostalim politopima (sa temenima iz iste klase ekvivalencije) ali tako da preko svakog pređemo tačno jednom.Neka je operator 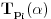 translacija za translacija za 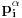 ( (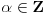 ) i neka je ) i neka je 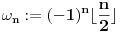 . Od sada pa na dalje za "kretanje" po hiperprostoru koristićemo nizove pomenutih translacija: . Od sada pa na dalje za "kretanje" po hiperprostoru koristićemo nizove pomenutih translacija: 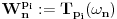 . Znači prvih . Znači prvih 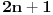 vrednosti za vrednosti za 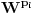 biće biće 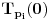 , ,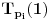 , ,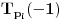 , ,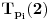 , ,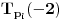 , , , ,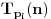 , ,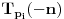 . .Ideja je da definisanje f-je izvršimo induktivno, i sada bi ovde lepo legla priča preko ordinala i afinih potprostora, koju ću ja pokušati da formalno (ali ne i suštinski Već smo uočili da svaki politop možemo predstaviti u obliku, 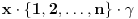 , pri čemu je , pri čemu je 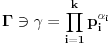 . Dakle, broju . Dakle, broju 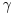 odgovaraju koordinate odgovaraju koordinate 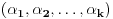 . Da bismo pratili "kretanje" politopa . Da bismo pratili "kretanje" politopa 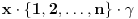 dovoljno je da pratimo koordinate broja dovoljno je da pratimo koordinate broja 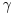 . Evo kojim redom će se vršiti dodefinisanje: . Evo kojim redom će se vršiti dodefinisanje: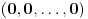 , ,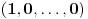 , ,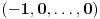 , ,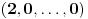 , ,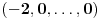 ... ...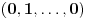 , ,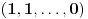 , ,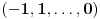 , ,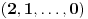 , ,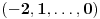 ... ...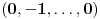 , ,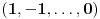 , ,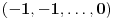 , ,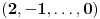 , ,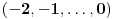 ... ...Dakle, u prvom koraku držimo fiksirane koordinate 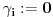 ( (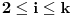 ) a za svako ) a za svako 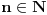 šetamo šetamo 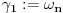 . Kada to završimo (joj šta bi Kroneker rek'o za ovo . Kada to završimo (joj šta bi Kroneker rek'o za ovo 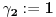 i i 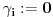 za za 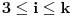 a opet prošetamo a opet prošetamo 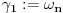 za svako za svako 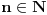 . Zatim, stavimo da je . Zatim, stavimo da je 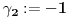 i i 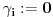 za za 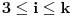 a opet prošetamo a opet prošetamo 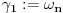 itd. itd.Mislim da je jasna šema: ako je izvršeno potpuno definisanje f-je za politope kod kojih je 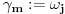 za sve za sve 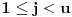 i i 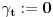 za za 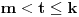 onda definišemo f-ju (rekurentno po dužini onda definišemo f-ju (rekurentno po dužini 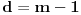 početnog dela početnog dela  -torke) i u svakom politopu kod koga je -torke) i u svakom politopu kod koga je 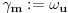 i i 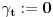 za za 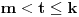 . .Da zaključimo: za sve je kriv Farenhajt [ uranium @ 25.01.2006. 13:30 ] @
Evo, da napišem i ono pomenuto state of the art rešenje
Neka je  prost broj i neka je za svako prost broj i neka je za svako 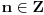 , , 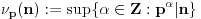 (znači (znači 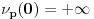 ). Sada možemo da proširimo domen f-je ). Sada možemo da proširimo domen f-je 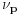 na ceo skup na ceo skup 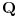 uzimajući da je za svako uzimajući da je za svako 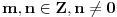 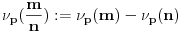 . .Za dato 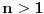 izaberimo prosto izaberimo prosto 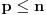 takvo da je takvo da je 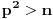 . To je uvek moguće: za . To je uvek moguće: za 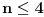 direktno proveravamo , a ako je direktno proveravamo , a ako je 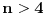 onda to sledi iz Bertrandovog postulata, jer mora da postoji prosto onda to sledi iz Bertrandovog postulata, jer mora da postoji prosto  za koje važi za koje važi 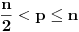 . .Neka je 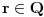 , uočimo da je , uočimo da je 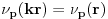 za svako za svako  i da je i da je 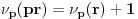 . .Neka je 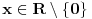 proizvoljno. proizvoljno.Skup 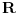 možemo da shvatimo i kao vektorski prostor nad možemo da shvatimo i kao vektorski prostor nad 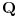 , a postojanje Hamel-ove baze nam daje i neku praktičnu korist od toga. Drugim rečima postoji neka familija realnih brojeva , a postojanje Hamel-ove baze nam daje i neku praktičnu korist od toga. Drugim rečima postoji neka familija realnih brojeva  , takva da za dato , takva da za dato  postoje jedinstveni brojevi postoje jedinstveni brojevi 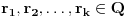 i jedinstveni vektori iz baze i jedinstveni vektori iz baze  , označimo ih sa , označimo ih sa 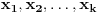 , takvi da važi , takvi da važi 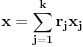 . .Najzad, definišimo 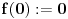 i i 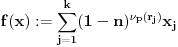 . .Proverimo da li su ispunjeni uslovi zadatka. Zbog jedinstvenosti reprezentacije, jasno je da važi 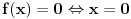 . . 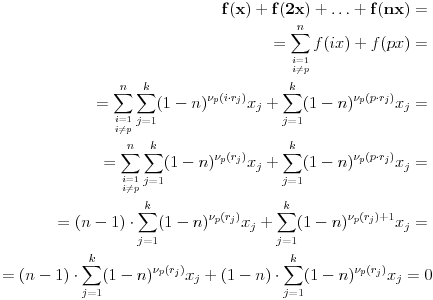 [Ovu poruku je menjao uranium dana 25.01.2006. u 15:02 GMT+1] [ Bojan Basic @ 29.01.2006. 00:52 ] @
Bravo za uraniuma!
Voleo bih samo da izdvojim ovaj detalj. Citat: uranium: Sada primetimo da prilikom svake translacije politopa 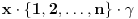 (pri čemu je (pri čemu je 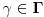 ) "za" broj ) "za" broj 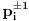 dobijamo novi politop koji će imati zajedničkih temena sa prethodnim, ali će (a to je bitnije) imati i barem jedno novo teme. Evo barem jednog novog temena: neka je dobijamo novi politop koji će imati zajedničkih temena sa prethodnim, ali će (a to je bitnije) imati i barem jedno novo teme. Evo barem jednog novog temena: neka je 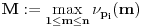 neka je neka je 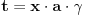 teme politopa kod koga je teme politopa kod koga je 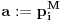 ako je translirano za ako je translirano za 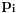 odnosno odnosno 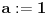 ako se radi o translaciji za ako se radi o translaciji za 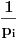 . Lako je videti da za celo . Lako je videti da za celo 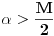 translati za translati za 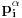 i i 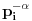 nemaju zajedničkih temena. A u slučaju kada je nemaju zajedničkih temena. A u slučaju kada je 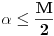 onda pomenuti translati imaju barem po jedno teme koje se nije "pojavilo" ni u jednom translatu za onda pomenuti translati imaju barem po jedno teme koje se nije "pojavilo" ni u jednom translatu za 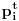 gde je gde je 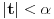 i i 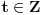 . .Jasno mi je šta pokušavaš da dokažeš, i intuitivno mi je jasno da to jeste zaista tako, ali ipak nisam uspeo da u potpunosti rastumačim tvoj način rezonovanja u ovom pasusu. Možeš li, molim te, malo da pojasniš? Za ostatak sam siguran da je dobro i još jednom sve čestitke. Citat: Farenhajt: Mene ovo neodoljivo podseća na jedan zadatak koji je uranium rešio (ne mogu sad da nađem topic), a tiče se funkcije na pravilnim poligonima. Ovde su poligoni, doduše, degenerisani, ali mislim da je princip vrlo sličan - tamo je dobijen rezultat da funkcija mora biti identički jednaka nuli, te se uslov 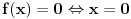 ne može zadovoljiti. ne može zadovoljiti.Pretpostavljam da misliš na ovu temu, ali, iskreno, mislim da su ova dva zadatka suštinski potpuno različiti. Citat: uranium: Da zaključimo: za sve je kriv Farenhajt :) da me nije prozvao - ne bih nikog ni mučio sa ovako "elegantnim" idejama :) Da zaključimo: za sve je zaslužan Farenhajt :) da te nije prozvao - ne bismo nikad imali prilike da pročitamo ovo zaista sjajno rešenje :) Rešenje koje sam ja imao u vidu kada sam postavio zadatak je ovo drugo po redu koje je dao uranium (sa Hamelovom bazom). To mi se tada jako svidelo, ali sada kada vidim ova dva remek dela jedno do drugog ne znam više šta da mislim :) Btw., uraniume, možeš li da mi kažeš, s obzirom na to što si rekao da rešenje nije tvoje, gde si ga pronašao? Za kraj, voleo bih da pomenem srkijevu ideju i Farenhajtovo pojednostavljenje. Prčkao sam nešto malo oko toga ali nažalost nisam uspeo ništa inteligentno da smislim, mada bi bilo jako lepo kada bismo i to mogli da dovršimo, pa ako je neko raspoložen neka pokuša. U svakom slučaju, meni je jako drago što sam konačno izbacio ovaj problem iz liste nerešenih zadataka. :) [ Farenhajt @ 29.01.2006. 14:47 ] @
Citat: Bojan Basic ...iskreno, mislim da su ova dva zadatka suštinski potpuno različiti Da, kad se zna rešenje, lako je videti da jesu Govorio sam samo o svom prvom utisku... sličnost.... asocijacije... ništa drugo (nisam nikad dublje uranjao u zadatak). [ uranium @ 29.01.2006. 17:02 ] @
@Bojan Bašić:
Sad tek vidim da je u onom pasusu koji si citirao ostala jedna nedovršena rečenica. Citat: 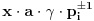 Ostatak uopšte nije teško obrazložiti, ali sam ja tu ulazio u neke potpuno nevažne detalje. Jedini rezultat koji mi je stvarno bio potreban je da pokažem da kada uzastopno generišem translacije za: 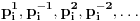 u svakom koraku dobijem jedno novo teme, tj. teme koje ne pripada ni jednom od prethodnih translata. u svakom koraku dobijem jedno novo teme, tj. teme koje ne pripada ni jednom od prethodnih translata.Neka je  . Pri translaciji za . Pri translaciji za 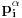 novo teme je novo teme je  , a ako se radi o translaciji za , a ako se radi o translaciji za 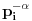 , onda je novo teme , onda je novo teme 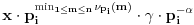 . . Ako, neko ipak želi detaljno objašnjenje onog citiranog dela (ili bilo kog drugog) - neka se ne ustručava da pita - rado ću pokušati da odgovorim. Hteo bih da se izvinim zbog dužine rešenja svima koji su ga pročitali (ili odustali od čitanja Citat: Bojan Basic: Rešenje koje sam ja imao u vidu kada sam postavio zadatak je ovo drugo po redu koje je dao uranium (sa Hamelovom bazom). To mi se tada jako svidelo, ali sada kada vidim ova dva remek dela jedno do drugog ne znam više šta da mislim Što se tiče onog drugog rešenja, bilo bi pošteno reći da je ono pronašlo mene a ne ja njega Nedugo posle postavljanja zadatka, bio sam u stanju da "nacrtam" rešenja za 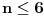 a uopštenje je bilo (i nažalost ostalo) previše induktivno za moj ukus. I tako sam počeo da tragam za nekom teoremom iz teorije grafova, mreža, algebre (dejstva grupa), koja bi mi elegantno potvrdila ono što sam već znao. Krenuo sam da smaram matematičke poznanike da li znaju nešto u tom pravcu - jedan od njih se zainteresovao za problem, pomenuo ga nekom profesoru, a ovaj ga je prepoznao iz nekog časopisa. I eto, posle nekih mesec-dva, imao sam prepričano rešenje po sećanju tog profesora a uopštenje je bilo (i nažalost ostalo) previše induktivno za moj ukus. I tako sam počeo da tragam za nekom teoremom iz teorije grafova, mreža, algebre (dejstva grupa), koja bi mi elegantno potvrdila ono što sam već znao. Krenuo sam da smaram matematičke poznanike da li znaju nešto u tom pravcu - jedan od njih se zainteresovao za problem, pomenuo ga nekom profesoru, a ovaj ga je prepoznao iz nekog časopisa. I eto, posle nekih mesec-dva, imao sam prepričano rešenje po sećanju tog profesora [ Bojan Basic @ 29.01.2006. 17:43 ] @
Da, stvarno si zakomplikovao taj pasus pa sam i ja odlutao pogrešnim tragom, sad vidim da je u suštini vrlo prosto :) Hvala na pojašnjenju.
Citat: uranium: Dakle, stvarno bih voleo da znam ko je taj "neznani junak" koji je to smislio - pa ako neko od vas ima pristup elektronskim arhivama matematičkih časopisa, neka javi... :) U stvari - Bojane - ti verovatno znaš o kome se radi? :) Hm... Nemam pojma. Koliko znam, ovo je originalno rešenje jednog ruskog profesora (Miša mu je ime, prezime ne znam), sumnjam da mislimo na istu osobu. Imam pristup solidnom broju elektronskih izdanja časopisa, pa ako otprilike znaš šta treba gledati javi mi i nije problem. Nego, da ja sada vama ispričam šta matematika ume da uradi od čoveka. Pomalo mi je žao da to kažem posle ovakvih rešenja, ali mislim da tema bez toga ipak ne bi bila kompletna. Sinoć sam relativno kasno iskucao prošlu poruku i legao da spavam. I tako meni još uvek igraju brojke pred očima, i padne mi na pamet potpuno elementarno rešenje, koje štaviše pronalazi funkciju  . Nažvrljam ja neke skice na papir čisto da ne zaboravim, a bio sam suviše umoran da proveravam. I ujutru ustanem, pogledam šta sam žvrljao, malo doradim detalje, i 'leba mi mog ono stvarno tačno rešenje! . Nažvrljam ja neke skice na papir čisto da ne zaboravim, a bio sam suviše umoran da proveravam. I ujutru ustanem, pogledam šta sam žvrljao, malo doradim detalje, i 'leba mi mog ono stvarno tačno rešenje!Dakle, za dato  sledeća funkcija ispunjava uslove zadatka: sledeća funkcija ispunjava uslove zadatka: Prvo treba dokazati da ova rekurzija uopšte ima kraja, a to nije teško. Za 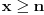 uvek možemo odabrati uvek možemo odabrati  takvo da je takvo da je  . Primećujemo da je kod onog rekurzivnog zbira . Primećujemo da je kod onog rekurzivnog zbira  od svakog sabirka manje od od svakog sabirka manje od 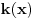 , pa ako funkciju „popunjavamo“ redom po , pa ako funkciju „popunjavamo“ redom po  nikad se nećemo zakucati. Za nikad se nećemo zakucati. Za 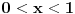 stvar je još jednostavnija: biramo stvar je još jednostavnija: biramo  tako da je tako da je 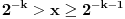 i tim redom popunjavamo. i tim redom popunjavamo.E sad, može li 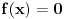 za za 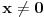 ? Ne može, jer se jednostavno može pokazati indukcijom po ? Ne može, jer se jednostavno može pokazati indukcijom po  da je da je 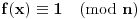 za sve za sve 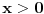 (tada, naravno, za (tada, naravno, za 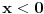 važi važi 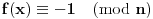 ). Drugi uslov zadatka takođe očigledno važi, i ostaje samo da kažem da sam stvarno razočaran što ovaj zadatak ima i prizemno rešenje. ). Drugi uslov zadatka takođe očigledno važi, i ostaje samo da kažem da sam stvarno razočaran što ovaj zadatak ima i prizemno rešenje.[Ovu poruku je menjao Bojan Basic dana 30.01.2006. u 02:16 GMT+1] [ uranium @ 30.01.2006. 00:47 ] @
Bojane, ako baš hoćeš, budi razočaran
U svakom slučaju, mislim da neću pogrešiti ako kažem da je zadatak bio fantastičan - jer nas je proveo kroz prelepe matematičke "predele" a čini se da nismo još ni videli sve što se nudi [ Bojan Basic @ 30.01.2006. 01:16 ] @
Citat: uranium: Bojane, ako baš hoćeš, budi razočaran :) - ali ja zaista mislim da je ovo najbolje rešenje do sad. Ne slažem se baš da je najbolje, mislim samo da je najjednostavnije, i u tom smislu sam rekao da sam razočaran. Posle svih onih dovijanja sa raznih strana i „ekstravagantnih“ ideja koje su stvarno prelepe, dođemo do ovako nečeg da kažem „seljačkog“ i onda se čini da je sve ono bilo za džabe (što svakako nije istina). Citat: uranium: U svakom slučaju, mislim da neću pogrešiti ako kažem da je zadatak bio fantastičan - jer nas je proveo kroz prelepe matematičke "predele" Stvarno sam i ja prezadovoljan, postavio sam zadatak da bih pokazao ono rešenje sa Hamelovom bazom i tad nisam mogao ni da zamislim do čega ćemo sve stići. Citat: uranium: a čini se da nismo još ni videli sve što se nudi :) U poverenju, ja još uvek ne odustajem od one srki-Farenhajtove ideje, bilo bi super da i to kompletiramo i ostaje samo da izdamo knjigu „Kojim sve putevima se može rešavati naizgled obična funkcionalna jednačina“ :) [ srki @ 30.01.2006. 21:42 ] @
Citat: A zar  ne zavisi od ne zavisi od  ? Tako makar pise ovde: ? Tako makar pise ovde:http://mathworld.wolfram.com/HamelBasis.html Ako  zavisi od zavisi od  onda mi je nekako sumnjivo ono resenje jer si ti koristio da je k jednako kod onda mi je nekako sumnjivo ono resenje jer si ti koristio da je k jednako kod  kao i kod kao i kod 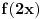 . .[Ovu poruku je menjao srki dana 30.01.2006. u 22:47 GMT+1] [ Bojan Basic @ 30.01.2006. 21:51 ] @
Zavisi, ali je isto za neki broj i sve njegove racionalne umnoške.
[ srki @ 30.01.2006. 21:58 ] @
Da, ocigledno je! Ko mi je kriv kada necu da razmisljam :-)
[ Bojan Basic @ 24.02.2006. 17:50 ] @
Citat: Bojan Basic: U poverenju, ja još uvek ne odustajem od one srki-Farenhajtove ideje, bilo bi super da i to kompletiramo i ostaje samo da izdamo knjigu „Kojim sve putevima se može rešavati naizgled obična funkcionalna jednačina“ :) Evo, i to je kompletirano, ali nažalost ne na način na koji sam se nadao. Naime, dokazaću da to ne može da prođe. Citat: Ako je 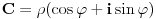 , onda je , onda je  , pa za , pa za 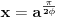 imamo imamo 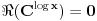 , a za , a za 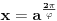 je je 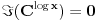 (gde je (gde je  osnova logaritma), i prvi uslov nije ispunjen. osnova logaritma), i prvi uslov nije ispunjen.Citat: Ni ova modifikacija ne prolazi. Ako je  , onda za , onda za 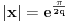 važi važi  , a za , a za  imamo imamo  , što je opet u suprotnosti sa prvim uslovom. , što je opet u suprotnosti sa prvim uslovom.[ srki @ 25.02.2006. 03:58 ] @
Citat: Napisao sam ja u mojoj poruci da to nece vaziti za neke diskretne vrednosti gde je funkcija nula za  i da se za te diskretne vrednosti moraju izabrati drugi brojevi (i rekurzivno dalje za neke ostale diskretne brojeve tj. odredjene racionalne umnoske tih brojeva)....Isto vazi i za Farenhajtov slucaj. i da se za te diskretne vrednosti moraju izabrati drugi brojevi (i rekurzivno dalje za neke ostale diskretne brojeve tj. odredjene racionalne umnoske tih brojeva)....Isto vazi i za Farenhajtov slucaj.[ Bojan Basic @ 25.02.2006. 18:56 ] @
Aha, onda sam pogrešno protumačio. Rekao si:
Citat: srki: E sada nam ostaje jos samo da resimo problem kada je f(x)=0 ali nisam dalje razmisljao o tome. Razumeo sam hoćeš da nađeš za koje vrednosti  je je 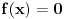 (i da li je to uopšte moguće za (i da li je to uopšte moguće za 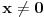 ). ).Moja namera prilikom pisanja jučerašnje poruke je bila samo da kompletiram pitanje za koje sam mislio da je ostalo bez odgovora (delom zato što nisam razumeo da se srki već osvrnuo na njega a delom zato što odgovor na njega Farenhajt u svojoj modifikaciji nije ni pominjao). Ukoliko sam bilo koga uvredio ili negde pogrešno postupio izvinjavam se, zaista mi to nije bila namera. [Ovu poruku je menjao Bojan Basic dana 25.02.2006. u 20:05 GMT+1] Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|