Koliko ja vidim i po rešenju su slična, tj. drugi je nešto komplikovaniji ali ideja je potpuno ista. Za sada ću napisati svoje rešenje prvog a drugi ću ostaviti još neko vreme da i neko drugi pokuša.

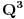
1. U svakoj lopti se nalazi bar jedna tačka koja pripada . Kraj.

Pretpostavljam da se pod smestiti podrazumeva da se lopte nemaj zajedničkih tačaka??

@Bojan

Svaka cast!

@utvara

Lopte se mogu dodirivati, ali se ne smeju preklapati. Slicno je i za slova P, ne smeju imati medjusobnih preseka.

Inace, prvi zadatak se moze postaviti i u zanimljivijoj formulaciji - "Dokazati da u svemiru postoji najvise prebrojivo mnogo planeta" (naravno, ako zanemarimo pretpostavke da prostor nije Euklidski, beskonacan, ...).

Ako posmatramo povrsinu slova P (zamislimo da je zatvoreno odozdole i da predstavlja pravougaonik) lako je videti da cemo uvek imati deo povrsine koji nije u preseku ni sa jednom drugom povrsinom od nekog drugog slova P. U tom delu povrsine postoji tacka koja pripada Q².

_{[Ovu poruku je menjao srki dana 01.09.2005. u 16:18 GMT+1]}

@srki
(zamislimo da je zatvoreno odozdole i da predstavlja pravougaonik)

Ne moze tako da se posmatra, u pitanju su slova P (oblik sastavljen od tri duzi koji nema povrsinu).

Znam, ja posmatram kao da ta povrsina odgovara tom slovu P. Deo te povrsine ce da pripada samo slovu P pa u tom delu mozemo naci tacku koja pripada Q².

To su zadaci iz jedne od zbirki zadataka Mile Mršević. Čak su i urađeni, ne u narkomanskom smislu.