Nisam matematičar visokog nivoa,ali rekao bih da je to funkcionalna analiza.

Nisam matematičar visokog nivoa, ali rekao bih da je to algebra.

Nisam matematičar visokog nivoa, ali rekao bih da su to Teorija skupova, i Matematička logika (Teorija modela, Teorija dokaza...). Sve to, naravno po mišljenju većine (poštenih) matematičara.

Međutim, ja verujem da skup teških matematičkih oblasti nema maksimum (doduše, to verovatno i nije skup), a što je još i gore, čini mi se da je skup teških problema po oblastima svuda gust

Nisam matematičar visokog nivoa, ali sam papagaj ;-b

Svakako je najteža oblast onu koju ne poznaješ. Ono što odlično poznaješ je izuzetno lagano, ma koliko se drugi trudili da te ubede suprotno.

Svi ste pogrešili. Po mišljenju velike većine matematičara najteža i najvažnija oblast matematike je

Ovo je lično moja teorema.

nisam matematičar visokog nivoa, ali bih rekao da teorema bez dokaza nije teorema, nego hipoteza...
dokazi, dokazi meni trebaju...

ali se slažem

Nadam se da to znači da ćeš nam prezentovati dokaz

Uh, pa to je tačno negacija moje theoreme. No, dokaži svoju teoremu da ne moram ja svoju :-)

Ne slažem se, štaviše čini mi se da su tvoja i Nedeljkova teorema ekvivalentne :)

Nedeljko, bilo bi interesantno da, u duhu tvoje teoreme, "čujemo" i od tebe: Koja je najteža i najvažnija oblast matematike?

Nisam matematicar visokog nivoa (ko bi rekao) ali mislim da je to algebra , pa geometrija (svejedno da li nacrtna ili projektivna ) .

Znate li vi koliko oblasti postoji u matematici?Pitam onako,cisto informativno...

To zavisi od osobe, ali mogu da ti kazem da najvise ljudi na matematickom fakultetu zagine na prvoj godini na Analizi ili na Algebri. Ako mene pitas (funkcionalna) Analiza, a znem neke koji ce ti reci Algebra :)

S. Kurepa (predavao mi je) u svom uvodu u Matematicku analizu I kaze da je ubedjen da vecina njih koji pohadjaju fakultete ne moze da shvati i usvoji pojam neprekidnosti funkcije. Slazem se sa njim. A neprekidnost funkcije je abeceda analize ...

Moje skromno misljenje je da je analiza teza za shvatanje nego algebra. Sto se tice matematickog fakulteta, mislim da treba dosta mozdane gimnastike da se provare divote tipa normirani prostori, funkcionalna analiza, parcijalne diferencijalne jednacine, matematicki model mehanike fluida ... srecom, to je iza mene :)

Meni licno je najteza numericka matematika, toliko je dosadna neinventivna da ne znam kakav covjek treba da budi da bi mu to bilo lako. Kad pogledam profesore na tom predmetu shvatim da moras da budes malo...

Ovi moji na faksu su totalno ispretumbali te matematike. Meni je funkcionalna analiza bio poslednji matematički ispit koji sam položio, a tek tada sam počeo da kontam neke osnovne pojmove vezane za analizu. Valjda zato što je rađena na neki algebarski način, ne znam. Poželeo sam da nakon toga prođem sve te matematike nanovo, kada mi je konačno ponešto i jasno. Ali blah, programer sam, realno su mi te analitičke stvari suvišne. Eventualno dobro dođu poneka diskretna matematika, logika i algebra i tako te boranije.

Numericke metode su interesantne jer ih mozes isprobati, a i 'videti' ako koristis grafiku. Tako da razumem one koji kazu: 'wow, ovo je brzo, wow, vidi kako brzo konvergira, cisto ludilo'.

Doduse, razumem i one koji ne mogu da se oduseve kada vide listu od 5000 brojeva koji lice jedan na drugi sve vise :)

Da, dodao bih i numericke metode resavanja parcijalnih diferencijalnih jednacina na listu. Takodje mislim da je Funkcionalna analiza preteska za fakultet, to je ipak za dublje proucavanje kasnije.

Teorema se vrlo lako dokazuje metodom anketitranja matematičara. Stepen korelacije između oblasti kojom se bave i oblasti koju smatraju najtežom i najvažnijom je skoro jedan.

A što se tiče najtežih predmeta na Matematičkom fakultetu u Beogradu, imajte u vidu da se analiza radi daleko najviše i najdublje. Evo nekih od ispita koje sam ja položio, kao i fonda časova koje sam imao iz njih:

Analiza:

1. Analiza I (4+4) 2 semestra
2. Analiza II (4+4) 2 semestra
3. Uvod u numeričku matematiku (2+2) 1 semestar
4. Analiza III (2+2) 2 semestra
5. Kompleksna analiza (2+2) 2 semestra
6. Diferencijalne jednačine (3+0) 2 semestra
7. Distribucije i parcijalne jednačine (2+2) 2 semestra
8. Diferencijalna geometrija (2+2) 2 semestra

Algebra:

1. Linearna algebra (4+4) 2 semestra
2. Algebra I (2+2) 2 semestra
3. Algebra II (2+2) 2 semestra

Geometrija:

1. Analitička geometrija (2+2) 2 semestra
2. Osnovi geometrije (2+2) 2 semestra
3. Nacrtna geometrija (2+2) 2 semestra

Topologija:

1. Topologija (2+2) 2 semestra
2. Algebarska topologija (2+0) 1 semestar

Sve ostale oblasti matematike sam učio na osnovnim studijama u okviru najviše jednog predmeta. Od onih koji se uče u okviru bar dva predmeta, analiza se uči u onoliko predmeta u koliko se uče sve ostale zajedno. Ukoliko se fond časova uzme u obzir, analiza je u još većoj prednosti (12:11). Predmet "diferencijalna geometrija" sam svrstao u analizu zbog izbora sadržaja iz diferencijalne geometrije koji se uče u okviru tog predmeta.

U školi je nejveći problem geometrija upravo zato što se najviše radi. Kada se neka oblast malo radi, uče se samo osnovni pojmovi i tehnike, pa to i nije tako teško. Kada se nešto radi više, ide se više u dubinu, pa je logično da se rade i složeniji sadržaji.

_{[Ovu poruku je menjao Nedeljko dana 10.09.2005. u 02:24 GMT+1]}

Svakako. Pogledaj prikačeni dokument pa prebroj :)

Postoji jednocifren broj grana matematike, kao što su analiza, algebra, geometrija, topologija, aritmetika, teorija brojeva, logika. No, svaka od njih se deli na svoje oblasti, na primer, analiza, na realnu analizu, kompleksnu analizu, funkcionalnu analizu, teoriju mere i integracije itd. ili kogika na teoriju skupova, teoriju modela, teoriju izračunljivosti, neklasične logike, Grane su "najkrupnije", pa ih ima najviše, ali užih oblasti ima daleko više. Kada se šalje članak nekom časopisu ili prijavljuješ saopštenje za neki skup, onda moraš da navedeš kojoj oblasti to pripada po klasifikaciji koju traži taj časopis/skup. Najrasprostranjenija klasifikacija je klasifikacija američkog matematičkog društva (ona je Windows), mada postoje i druge (one su Linux). Zvanična klasifikacija matematike po američkom matematičkom društvu se menja na nekoliko godina zbog stalnog razvoja matematike, a na internetu je možeš naći ako mašini za pretraživanje zadaš frazu "AMS subject classification". AMS potiče od American Mathematical Society (Američko matematičko društvo). Bojan Bašić ti je poslao PDF verziju, ali mislim da je HTML vetzija zgodnija za pretraživanje.

Basicu jer bas moram da brojim?...
Pozdrav i hvala na informaciji.

Poškakljite me da se nasmijem...

Zaboravio sam na Analizu . To su bila horor vremena kada sam se mucio time. hvala Bogu sto je to daleko iza mene.

Nažalost, moram se složiti da je upravo to utisak koji se može steći na predavanjima iz numeričke na našim fakultetima...



Ne želim ni na koji način da umanjim značaj numeričke matematike (šta više ima toliko i teorijiskih i praktičnih problema koje, u ovom trenutku, ne bismo umeli da rešimo da nije numeričkih metoda) ali kakav god algoritam smislili za aproksimaciju bilo čega, u principu je trivijalno konstruisati primer matematičkog objekta čije se osobine drastično razlikuju od onih koje bi njegova aproksimacija predvidela.

Evo jednog primera koji ilustruje nemoć aproksimacija:

Uz pomoć bilo kog matematičkog programa, nacrtati grafik funkcije

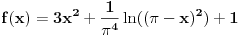
i uveriti se da u tački f-ja ima vertikalnu asimptotu.

Sve u svemu, ja bih numeričku matematiku radije zvao matematička numerologija.

Poenta teme koju sam postavio je bila da napravim matematički vic zasnovan na zbilji. To je pre svega bila moja reakcija na onaj glupavi 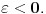No, očigledno me niko nije shvatio.

A što se numeriške analize tiče, ona je isto toliko strogo zasnovana koliko i bilo koja druga oblast matematike.

Makar sam uspeo da skontam dokaz tvoje teoreme :-)

Mislim da je najteža ona oblast za koju nemaš vremena da se pripremiš, ili ona za koju nemaš dobru literaturu, a najgore je i jedno i drugo... :o)

Jedan od odgovora je ona oblast u kojoj ima najvise neresenih problema.

Ili gde dokaze teorema merimo kilometrima.

Po meni, onako laicki, kombinatorna geometrija.


_{[Ovu poruku je menjao DDMM dana 13.09.2005. u 04:04 GMT+1]}

Zanimljivo je da razni ljudi ovde razumeju pitanje na razne nacine. "Koji je najtezi kurs na fakultetu" ili "koja je najteza oblast za bavljenje naucnim radom"?

Mene su na fakultetu verovatno najvise namucili numericki predmeti, ali to nije do same oblasti nego do nacina poducavanja i provere znanja koji su se koristili.

Kad sam rekao da je algebra najteza, racunao sam teoriju skupova i logiku kao podgrane algebre. Mozda to i nije bas dobar pogled.

Zaboravio sam da dodam jednu zanimljivu pricu s Matematickog fakulteta u Beogradu. Radi se o anegdoti, ali vrlo uverljivoj, i ubedjen sam da je istinita. Cak i ako se dogadjaji o kojima govori i nisu stvarno odigrali, to ne umanjuje ostrinu naravoucenija.

Pre par godina jedan asistent (danas vec profesor) je sastavio, da li ozbiljno, iz shege ili kao misaoni eksperiment, spisak od deset pitanja o najosnovnijim pojmovima matematike koja se izucava na fakultetu. Sta je ravnomerna neprekidnost? Kako glase Silovljeve teoreme? Sta su P i NP klase problema? Primetite da se ne radi o detaljima nekih dokaza, nego o elementarnoj obavestenosti o stvarima koje se uce kroz te cetiri godine (obicno u praksi sedam-osam).

Navodno je pokazao taj spisak nekim kolegama i pitao "Sta mislite, ako bismo postavili ovo kao test diplomcima, koliko njih bi polozilo?" i svi su se iskreno nasmejali. Onda je jedan od kolega pitao "A ako bi dao taj test Nastavno-naucnom vecu?" ... i svi su prestali da se smeju.

(Implicitno je u prici to da, da biste prosli test, morate da odgovorite na sva pitanja. Ipak su to, na kraju krajeva, fundamenti predmeta koje ste vec polozili.)

Ni ja nisam kako ono rekose "matematicar visokog nivoa", upoznao sam je na ETFu a to je koliko kapiram ipak iscasen pogled na matematiku. Najteza mi je KOMPLEKSNA ANALIZA. Koliko sam shvatio veoma nerazvijena mada se divim ljudima da su i ovoliko uspeli da je razviju. Radili smo samo elementarne sablonizovane stvari ali dovoljno da skapiram koliko to tesko moze da bude!

Svakako da je najteža ona oblast koju ne znam...

Kao student fakulteta elektrotehnike,mogu navesti kao najmanje razumljiviju i najnepristupačniju oblast(koja unatoč svim naporima ostaje takva)vezanu za Nizove.Meni,a vjerovatno i ostalima.