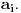Pretpostavimo suprotno da je n>m.
Tada b1...bm generise v.p. V tj. taj sistem sadrzi bar jednu bazu (ako je p broj vektora baze tada je m>=p) i a1,...,an sistem lin. nez. vektora tog prostora. a posto je baza v.p. najveci broj lin. nezavisnih vektora u tom prostoru dobijamo da je p>=n => m>=p>=n sto je suprotno pretpostavci da je n>m dakle mora biti m>=n.

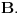
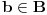
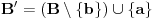
Lema: Neka je bilo koji nenula vektor i bilo koji skup vektora takav da je vektor u linearnom omotaču skupa Tada postoji vektor takav da za skup važi

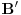
a) Skupovi i imaju iste linearne omotače.
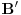
b) Skup je linearno nezavisan ako i samo ako je skup linearno nezavisan.

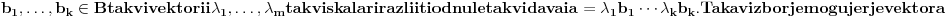
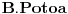
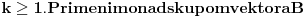
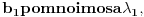
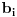
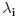
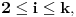
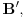
Dokaz: Neka su u linearnom omotaču skupa nije nula vektor, biće sledeće elementarne operacije: najpre vektor a potom dobijenom vektoru dodajmo vektor pomnožen sa za sve ako takvih ima. Rezultat će biti skup a osobine a) i b) će biti posledice činjenice da je skup

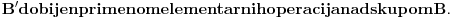
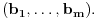
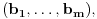
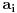
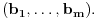
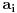
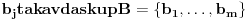
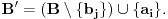
Sada se tvoje tvrđenje dokazuje indukcijom po broju vektora iz sistema koji se ne pojavljuju u sistemu Ako među vektorima nema onih koji se ne pojavljuju u sistemu onda tvrđenje svakako važi. 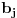U suprotnom, neka se vektor ne pojavljuje u sistemu Pošto su vektori linearno nezavisni, ne može biti nula vektor, pa će postojati neki vektor ima isti linearni omotač kao skup Sada tvrđenje dokazuje primenom induktivne pretpostavke na sistem i sistem koji se dobija zamenom vektora u sistemu vektorom