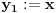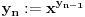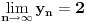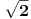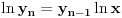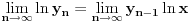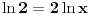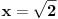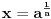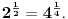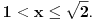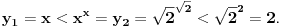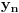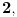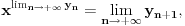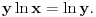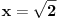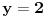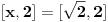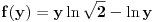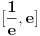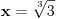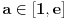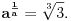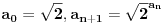Neka je bilo koji realan pozitivan broj.
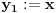
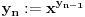
Definišemo niz i (za ).
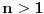
Onda se zadatak svodi na pitanje, za koje realno važi:
.
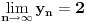
Ako takvo postoji, dokazaćemo da je ono jednako .

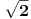
Kako je ,
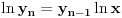
imamo da važi:
,
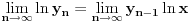
pa na osnovu neprekidnosti logaritamske funkcije i uslova zadatka važi i
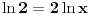
, odakle dobijamo da je .

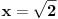
(Jasno je da se u zadatku, broj 2 može zameniti bilo kojim pozitivnim realnim brojem npr. , s tim da je onda rešenje )

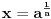
Napomenuo bih da upotreba logaritamske f-je nije ključna tj. da se uz iste pretpostavke moglo i direktno doći do istog zaključka, ali uz korišćenje neprekidnosti stepene f-je, pa pošto je uobičajano da se ova poslednja f-ja definiše preko logaritamske, odlučio sam se za logaritmovanje...

Očigledno je da egzistencija rešenja nije dokazana, pa pokušaj to prvo sam.


_{[Ovu poruku je menjao uranium dana 12.10.2005. u 14:18 GMT+1]}

Pripazi samo na činjenicu da je

Neka je Tada je Sada se indukcijom dokazuje da je niz rastući i da je odozgo ograničen sa pa je konvergentan. Za njega važi da je , pa za njegov limes važi Za je jedno rešenje. Na ovde interesuju samo rešenja u intervalu Na tom intervalu je funkcija monotona, pa ne može imati više od jedne nule.

Broj se mogao zameniti sa bilo kojim brojem u intervalu , ali se nije mogao zameniti sa jer bi se za dobio niz koji bi konvergirao ka broju takvom da je

A da li može ovako:

pretpostavimo da je a=((...x**x)**x)**x..... za vrlo velik broj stepenovanja. Ako a stepenujemo još jednom, t.j. b=a**x, tada mora biti b=a, pod uslovom da cela stvar konvergira. Ili, a**x=a. Ovo će biti tačno samo ako je x=1.

A takođe i ako je x=0.

A evo i male glavlomke za preko vikenda: Zašto Uraniusovo rešenje x=sqr(2) (koren iz dva) nije tačno? Ako pokušate da računate dobićete sledeću tabelu:

Iteracija: 1 x^x:1.63252691943815
Iteracija: 2 x^x:2
Iteracija: 3 x^x:2.66514414269023
Iteracija: 4 x^x:4
Iteracija: 5 x^x:7.10299330131602
Iteracija: 6 x^x:16
Iteracija: 7 x^x:50.4525138385403
Iteracija: 8 x^x:256.000000000001
Iteracija: 9 x^x:2545.4561526281
Iteracija: 10 x^x:65536.0000000006
Iteracija: 11 x^x:6479347.02495228
Iteracija: 12 x^x:4294967296.00009
Iteracija: 13 x^x:41981937869758.1
Iteracija: 14 x^x:1.84467440737104E+19
Iteracija: 15 x^x:1.76248310730025E+27
Iteracija: 16 x^x:3.40282366920975E+38
Iteracija: 17 x^x:3.10634670351879E+54
Iteracija: 18 x^x:1.15792089237344E+77
Iteracija: 19 x^x:9.64938984246241E+108
Iteracija: 20 x^x:1.34078079299496E+154
Iteracija: 21 x^x:9.3110724331823E+217

iz koje se vidi da proces ne konvergira. ( a kada je a<1, npr. x=0.5**2, ceo proces konvergira ka 1).

Zato sto si zanemario da je stepenovanje desno asocijativno :).

Ti si sigurno napisao nesto kao :



A treba ipak:



Dakle a^b^c je u stvari a^(b^c) a ne (a^b)^c. Cak se prica da Wirth nije ubacio stepenovanje u pascal zbog moguce neracionalne primene i zbog toga sto je jedina desno asocijativna (pa bi bunila ljude).

I kakva se onda dobije tabela?

Prvih 75 iteracija izgleda ovako:

1.41421356
1.63252692
1.76083956
1.84091087
1.8927127
1.9269997
1.95003477
1.96566489
1.97634175
1.9836684
1.98871177
1.99219088
1.99459445
1.99625667
1.997407
1.99820348
1.99875513
1.99913731
1.99940212
1.99958562
1.9997128
1.99980094
1.99986202
1.99990436
1.99993371
1.99995405
1.99996815
1.99997792
1.9999847
1.99998939
1.99999265
1.9999949
1.99999647
1.99999755
1.9999983
1.99999882
1.99999918
1.99999943
1.99999961
1.99999973
1.99999981
1.99999987
1.99999991
1.99999994
1.99999996
1.99999997
1.99999998
1.99999999
1.99999999
1.99999999
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0

(Čujem neku klepetušu u daljini... )

Tako je, svaka čast! Dodatak za Farenhajta: Pričuvaj kokice, ptičji grip nam se približava!

_{[Ovu poruku je menjao Lobacev dana 24.02.2006. u 15:24 GMT+1]}