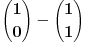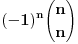5. zadatak pod a tvrdi da je zbir prvih m neparnih prirodnih brojeva jednak kvadratu broja m. Možda nisi dobro zapisao razvijeni oblik? Ovo je tačno i lako se dokazuje indukcijom.

5. zadatak pod b je isto u redu, hajde da vidimo šta si dobio kada si to razvio u sumu, možda negde grešiš.

Moja greška, tek sam kasnije svatio da u bazi indukcije za n=2 nisam zbrajao prva dva.

Hvala na odgovoru.

<<<<<<<<ipak imam još jedno pitanje:
Dokažite da vrijedi:

Neka j ono nad ili povrh predstavljno znakom #.

Pa ide zdatak...

(n#0) - (n#1) + (n#2) -...+ (-1)ⁿ (n#n) = 0.

E sad i ovo sam pokušao ali u bazi indukcije za n=1 imam :

(1#0) = 0. Kako je to moguće. Po pravilu je (n#0)=1

Ovde nisi dobro odredio izraz za n=1. Treba da bude:

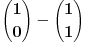
a to jeste nula. Kada ustanoviš kako izgleda razvijena suma, da bi dokazao prvi uslov uvek zamenjuj n u opšti član da vidiš sa kojim elementom ti se završava taj iskaz. Ovde ti je poslednji član

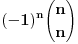
dakle, za n=1 dobijaš razliku navedena dva binomna koeficijenta, a ti si uzeo samo prvi.

Hvala Lampica!