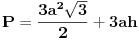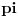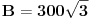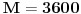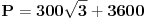Pravilna cetvorostrana piramida u osnovi ima kvadrat.

P=B+M=a^2 + 2*a*h
B-povrsina osnove,M-povrsina omotaca,a-ivica osnove,h-visina bocne strane

V=B*H/3=a^2*H/3 H=sqrt(h^2 - (a/2)^2)
H-visina piramide

Pravilna sestostrana:

P=B+M=3*a^2*sqrt(3)/2+3*a*h
V=B*H/3=a^2*sqrt(3)/2*H

Valjak:

P=B+M=2*PI*r^2 + 2*PI*r*H=2*PI*r(r+H)
V=B*H=PI*r^2*H
H-visina valjka,r-poluprecnik osnove valjka

Kupa:

P=B+M=PI*r^2 + r*PI*s
r-poluprecnik osnove kupe,s-duzina bocne ivice

V=B*H/3=PI*r^2*H/3 H=sqrt(s^2 - r^2)

Za cetvorostranu piramidu ok, samo imam par pitanja za ostale...

..

sqrt(3)/2+3 - ne razumem sta je ovde pod korenom milsim ja napisem koren iz 3/2 al mi je to neko nelogicno jer koren iz 3 je 1.73 ne znam dal to tako treba uvek mi izlaze decimalni brojevi?

i za valjak ne razumem ono sa PI recimo dobijem da treba da izracunam
V=B*H
V=4pi * 50
to je valjda 200pi ?

P=B+m
P=4pi + 200
P=?

Sta da radim sa tim pi jel se on menja sa nekim brojem kako?

Hvala ti unapred

A joj...
Ovako...
Imaš pod korenom samo trojku. Ne razumem zašto si napisao sqrt(3)/2+3 kad ovo +3 na kraju nema veze sa prethodnim delom. Evo ti ga ovako napisano, možda će ti biti lakše.



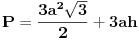
Mada, trebao bi da znaš koja operacija ima prednost nad kojom. Znači čita se:
Tri puta a na kvadrat, puta koren iz tri, pa sve to kroz dva, pa još plus tri puta a i puta h.

I ako ti smeta koren iz 3 onda moraš da ga računaš sa decimalama, mada je praksa da se ostavlja sa korenom.

Jasnije?

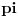
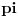
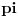
A tek na drugo pitanje ne znam šta da ti kažem. Kako si mogao da stigneš do druge godine srednje ako ne znaš šta je Pi . Najjednostavnije rečeno Pi je odnos obima i prečnika svakog kruga i iznosi približno 3.14! Mada je i ovde praksa da se osvalja rezultat sa , jer ima beskonačno mnogo decimala.



_{[Ovu poruku je menjao del-boy dana 17.10.2005. u 23:14 GMT+1]}

edit: TeX

_{[Ovu poruku je menjao del-boy dana 17.10.2005. u 23:17 GMT+1]}

Ajde ovako da ne razvlacim...

1) Izracuneaj P i V cetvorostrane piramide ako je:
a=10m(osnovna ivica) bocna ivica s=13m

2) Sestostrana piramida P=? V=?
a=10cm s=13cm

3) Odrdi sve nepoznato (valjak):
r=2 M=20pi

4) Odredi nepoznato (kupa)
r=5 H=12

Pa neće ti ovde niko raditi domaći...
Ajde ti lepo počni da radiš pa ako zapneš opet pitaj.

btw. sve ove formule imaš u knjizi za osmi razred osnovne škole pa pogledaj malo!

nisam ni ocekivao, pa konkretno kod sestostrane piramide
a=10
s=13
P=?
V=?
dobijem da je P=495+sqrt(3) jel to kraj?

jer dobijam da je M=195+sqrt(3)
i da je B=300

Iako sad žurim, ali koliko sam ovako na brzinu naračunao , a , što znači da je površina .
Mada možda sam pogrešio u računanju, proveriću opet kad dođem kući!

s=13, a=10, P=?

P=B+M;
B=6*(a^2*sqrt(3)/4); gde je "a^2*sqrt(3)/4" povrsina jednakostranicnog trougla a ne /2 sto mnogi grese
M=6*(a*h/2); gde je "a*h/2" povrsina jednakokrakog trougla odnosno bocnih strana

Nepoznato nam ostaje samo h, koje izracunamo iz pitagorine teoreme:
s^2=h^2+a^2/4; gde je "a^2/4" kvadrat polovine stranice a
h^2=169-25
h^2=144
h=12

Tada je:

B=6*(100*sqrt(3)/4)=150*sqrt(3)
M=6*(10*12/2)=360

I

P=150*sqrt(3) + 360