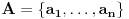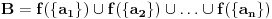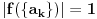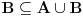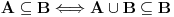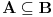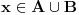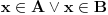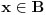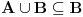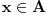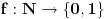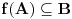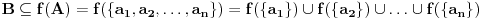[ pistareale @ 22.10.2005. 18:44 ] @
| Molio bi ako mi netko moze rijesiti slijedece dokaze a) Imamo f:A->B, gdje je A konacan skup, funkcija f surjektivna. Pokazati da je B konacan skup. b) Pokazati da za bilo koja dva skupa A,B ove trvdnje su ekvivalentne A(_B AuB=B c) Je li skup svih funkcija f:N->N prebrojiv ? Svaka pomoc dobrodosla.Hvala |