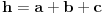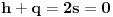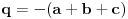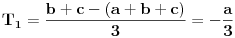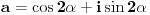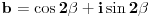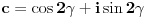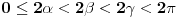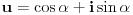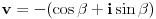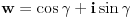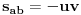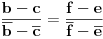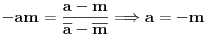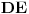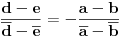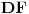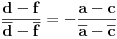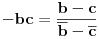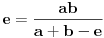[ Bojan Basic @ 25.10.2005. 22:03 ] @
| Kompleksni brojevi su vrlo moćna stvar prilikom rešavanja mnogih geometrijskih zadataka. Mana ovakvog pristupa je što se često dolazi do nekog dugačkog računa, a prednost je što se geometrijski zadaci od kojih neki mogu zahtevati neku ideju koju je teško uočiti na ovaj način svedu na čist šablon. Pa, ko voli nek izvoli :) Da ja ne bih tupio sa nekom teorijom kada su to radili mnogi ljudi pre mene, prikačio sam jedan dokument gde su objašnjene osnove (na kraju teksta, nakon zadataka), a sve ostalo će doći na svoje mesto nakon vežbanja, vežbanja i samo vežbanja. Naravno, ukoliko bude bilo nekih pitanja u vezi sa ovom tematikom, slobodno ih postavite ovde. |