[ Bojan Basic @ 26.10.2005. 23:08 ] @
|
[ noviKorisnik @ 26.10.2005. 23:36 ] @
Da krenem pešački, indukcijom :-)
n = 1 -- izem ga, ovo je 0 ili 1, pre će biti 1, verovatno nije bitno n = 2 -- 3 linije n = 3 -- 5 linija (baš neka indukcija, crtam spirale u glavi :-) n = 4 -- 7 linija ... recimo... 2n - 1 [ uranium @ 26.10.2005. 23:40 ] @
Samo da proverim da li sam dobro shvatio:
ako dobijenu strukturu (posle povlačenja svih duži) shvatimo kao graf, da li je onda dozvoljeno da neki od čvorova ima stepen veći od 2? I da li će se pod duži, podrazumevati grana grafa ili klasična geometrijska duž? [Ovu poruku je menjao uranium dana 27.10.2005. u 02:21 GMT+1] [ Bojan Basic @ 27.10.2005. 11:30 ] @
Citat: noviKorisnik: recimo... 2n - 1 Nije baš toliko jednostavno - može to još manje :) Citat: uranium: Samo da proverim da li sam dobro shvatio: ako dobijenu strukturu (posle povlačenja svih duži) shvatimo kao graf, da li je onda dozvoljeno da neki od čvorova ima stepen veći od 2? Nisam siguran da li pod čvorom podrazumevaš date početne tačke ili čvorom nazivaš i svaki presek te izlomljene linije sa samom sobom, ali i u jednom i u drugom slučaju je dozvoljeno. S druge strane, jedna duž može da pokrije i više tačaka, odnosno date tačke ne moraju da predstavljaju krajeve duži već mogu i da leže na njoj. Citat: uranium: I da li će se pod duži, podrazumevati grana grafa ili klasična geometrijska duž? Klasična geometrijska duž. Znači, ako se dve duži koje su deo te izlomljene linije preseku, njih i dalje brojimo kao dve duži (a ne tri ili četiri). [ uranium @ 28.10.2005. 14:30 ] @
Verovatno nije u redu, ali makar da krenemo sa mrtve tačke
Ako je dozvoljeno proći jednom istom granom po jednom u svakom smeru, onda je minimalan broj duži 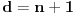 , za , za 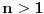 . .Jer, budući da jedna duž može da sadrži najviše  tačaka, ako bi bilo tačaka, ako bi bilo 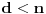 , onda bi bilo , onda bi bilo 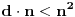 , pa nebismo pokrili sve tačke, znači mora biti , pa nebismo pokrili sve tačke, znači mora biti 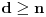 . Međutim, ne može biti . Međutim, ne može biti  , jer to bi značilo da svaka duž mora imati po , jer to bi značilo da svaka duž mora imati po  različitih tačaka pa bismo onda imali različitih tačaka pa bismo onda imali  komponenata povezanosti, a nama treba jedna komponenta povezanosti. komponenata povezanosti, a nama treba jedna komponenta povezanosti.Dakle, 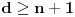 . .E sad, da vidimo da je uvek moguće napraviti put dužine  . .Pošto me mrzi da crtam, evo primera za 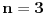 , a ostali slučajevi se rešavaju potpuno analogno. , a ostali slučajevi se rešavaju potpuno analogno.Označimo čvorove kao: 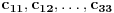 , onda je traženi put: , onda je traženi put: 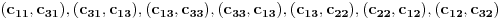 . .Ukratko, crtež nastaje tako što povučemo po jednu duž po svim: ili kolonama ili vrstama, a zatim i jednu duž po: ili sporednoj ili glavnoj dijagonali. [Ovu poruku je menjao uranium dana 28.10.2005. u 15:38 GMT+1] [ Bojan Basic @ 28.10.2005. 21:41 ] @
Citat: Jednom granom je dozvoljeno proći samo jednom bez obzira na smer. Znači, stavimo olovku na jedno mesto i, ne podižući je, povlačimo je po papiru pri čemu ne smemo istu liniju crtati dva puta (ali smemo da sečemo). NoviKorisnik je, čini mi se, dobro shvatio šta se traži u zadatku, ali mu rezultat nije dobar. [ Shadowed @ 29.10.2005. 06:41 ] @
Hmm, ja znam kako da uradim za n=3 sa 4 duzi ali nikako da to primenim na n>3...
[ Leftist @ 29.10.2005. 12:50 ] @
ja sam n=3, 4, 5 resio sa 4, 6 i 8 duzi, sto je za 1 bolje od novoKorisnikovog resenja, znam kako sam dosao do toga, ali ne znam kako da resenje uopstim za bilo koje n...
(hint: duz ne mora da se zavrsi sa ivicom kvadrata) [ noviKorisnik @ 29.10.2005. 17:01 ] @
Ja baš nisam uspeo da nađem rešenje od 4 poteza za n=3. Okačite sliku, please...
[ uranium @ 29.10.2005. 18:59 ] @
Valjda može ovako:
[Ovu poruku je menjao uranium dana 30.10.2005. u 01:05 GMT+1] [ Leftist @ 29.10.2005. 23:21 ] @
Hoces reci ovako:
[Ovu poruku je menjao Leftist dana 30.10.2005. u 00:23 GMT+1] [ uranium @ 30.10.2005. 00:30 ] @
Naravno, može i tako
[Ovu poruku je menjao uranium dana 30.10.2005. u 01:41 GMT+1] [ Bojan Basic @ 30.10.2005. 00:54 ] @
Što nekad mrzim sebe kad loše napišem postavku pa posle moram da se ispravljam/dopunjujem :)
Sličica koju je uranium ostavio nije korektna jer svaku duž moramo nacrtati odjednom, ne može prvo pola, pa onda nacrtamo nešto drugo, i onda druga polovina (kao što su na njegovom crtežu duži 1-7 i 3-5). U ovom slučaju to se računa kao 6 duži (mada priznajem da u postavci nisam precizno razjasnio taj deo). Možda je najjednostavnije reći da brojimo koliko načinimo skretanja olovkom (pri čemu postavljanje olovke na papir brojimo kao prvo skretanje, čisto radi konzistentnosti sa ovom prethodnom definicijom). Bilo kako bilo, nadam se da je konačno jasno kako linija treba da izgleda i šta se od svega toga broji. Ono što sam zaista imao u vidu za 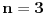 je rešenje koje je Leftist dao (mogu da kažem da se ovaj slučaj već pojavljivao na ES-u, videti http://www.elitesecurity.org/tema/125614, ali nisam hteo odmah da ostavljam link da ne upropastim zabavu). Rešenje ovog slučaja je korak unapred, preostaju nam još dve stvari: da nađemo konstrukcije za je rešenje koje je Leftist dao (mogu da kažem da se ovaj slučaj već pojavljivao na ES-u, videti http://www.elitesecurity.org/tema/125614, ali nisam hteo odmah da ostavljam link da ne upropastim zabavu). Rešenje ovog slučaja je korak unapred, preostaju nam još dve stvari: da nađemo konstrukcije za 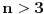 i da dokažemo da ne možemo bolje od toga :) i da dokažemo da ne možemo bolje od toga :)[ noviKorisnik @ 30.10.2005. 10:59 ] @
Evo konstrukcije za n > 2 i 2(n - 1) poteza . . . Dalje se samo nastavlja po spoljnoj spirali, za svaku sledeću brojku dimenzije doda se po još 2 duži. Eto, dokazano je da može bolje od onoga što sam prvo rekao, sad još da se dokaže da ne može bolje od ovoga (ili opet da može :-))) [ noviKorisnik @ 16.09.2011. 11:42 ] @
Ova tema još uvek stoji izlistana među nerešenim zadacima :-)
Potražio sam ima li odgovora na mreži... Evo jedne stranice koja obrađuje temu: Most Wanted Puzzle Solutions - The Nine Dot Puzzle. Pored nekoliko zanimljivih razmatranja, na kraju se dotiče i generalizacije problema, gde se navodi da se minimalno rešenje poklapa s prethodnom pretpostavkom, iako ne vidim formalni dokaz tvrdnje. [ Bojan Basic @ 16.09.2011. 11:53 ] @
Citat: noviKorisnik: ...gde se navodi da se minimalno rešenje poklapa s prethodnom pretpostavkom, iako ne vidim formalni dokaz tvrdnje. Dokaz optimalnosti rešenja i jeste ono što nedostaje u ovoj temi, i zbog čega ona i dalje stoji na listi nerešenih zadataka. [ kaćunčica @ 20.09.2011. 14:28 ] @
Padalo mi je na pamet da polazne tačke posmatram kao kvadratnu matricu, pa onda donosim zaključke o indeksima koji su na istoj duži... Sreća da je danas četvrti dan, pa ćemo videti rešenje :)
[ Bojan Basic @ 21.09.2011. 20:44 ] @
Evo dokaza. Izvinjavam se zbog kašnjenja od celog jednog dana, kako je kaćunčica to strogo izbrojala.
Pretpostavimo da postoji  redova redova  kolona na kojima ne leži nijedno parče uočene putanje. Ako je kolona na kojima ne leži nijedno parče uočene putanje. Ako je 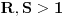 , mreža veličine , mreža veličine 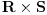 koju oni formiraju ima koju oni formiraju ima 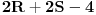 rubne tačke. Svaka koso parče putanje pokriva najviše dve od ovih tačaka. Dakle, putanja ukupno mora imati bar rubne tačke. Svaka koso parče putanje pokriva najviše dve od ovih tačaka. Dakle, putanja ukupno mora imati bar 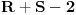 kosih parčića, kosih parčića, 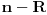 horizontalnih i horizontalnih i 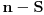 vertikalnih, što čini ukupno bar vertikalnih, što čini ukupno bar 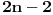 parčeta. Ako je parčeta. Ako je  ili ili  jednako jednako  ili ili  , tada se lako proterava da putanja mora imati bar čak , tada se lako proterava da putanja mora imati bar čak 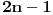 parče. parče.To je sve. 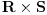 koje nisu na rubu) na kraju ipak ispostavi da nismo preterali s aproksimacijama. koje nisu na rubu) na kraju ipak ispostavi da nismo preterali s aproksimacijama.Dakle, zahvaljujući inicijativi novogKorisnika, zadatak je najzad skinut s liste nerešenih. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|