[ del-boy @ 26.10.2005. 23:47 ] @
|
[ uranium @ 27.10.2005. 00:12 ] @
Sam si rekao da su svi konvergentni nizovi ujedno i Košijevi, pa pošto niz 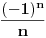 teži nuli, znači da je i Košijev. teži nuli, znači da je i Košijev.Inače, za realne nizove važi i obrnuto, tj. da je svaki Košijev ujedno i konvergentan. Pa tako dobijamo, da se u slučaju realnog prostora (sa uobičajenom metrikom), skup Košijevih i skup konvergentnih nizova poklapaju. Dakle, ako hoćeš da vidiš primer "analitički" zadatog niza koji nije Košijev, moraćeš da uzmeš neki divergentan niz (ili da pređeš u neki interesantniji metrički prostor [ uranium @ 27.10.2005. 00:33 ] @
Evo jednog primera (inspiracija je verižni razlomak)
neka je   -ta aproksimacija broja -ta aproksimacija broja 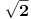 verižnim razlomkom, znači: verižnim razlomkom, znači: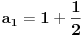 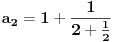 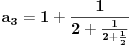  očigledno je da je 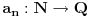 , tj. , tj.  je niz racionalnih brojeva. je niz racionalnih brojeva.Dakle, posmatrajmo 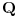 kao metrički prostor (sa uobičajenom metrikom), pošto znamo da verižni razlomak konvergira ka kao metrički prostor (sa uobičajenom metrikom), pošto znamo da verižni razlomak konvergira ka 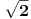 u metričkom prostoru u metričkom prostoru 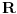 , onda je on i Košijev ( u , onda je on i Košijev ( u 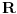 ), pa kako je metrika u ), pa kako je metrika u 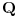 restrikcija metrike iz restrikcija metrike iz 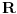 , onda je (budući da je , onda je (budući da je  racionalan niz) on Košijev i u racionalan niz) on Košijev i u 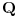 . A kako . A kako 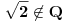 , on divergira u , on divergira u 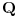 Znači, "seljačkim" jezikom kod Košijevog niza članovi se sve više i više "zgušnjavaju" (postaju sve bliži jedan drugom), ali, zavisno od prostora u kome sve posmatraš, to ne mora biti dovoljno za konvergenciju. [Ovu poruku je menjao uranium dana 27.10.2005. u 02:00 GMT+1] [ peddja_stankovic @ 27.10.2005. 05:40 ] @
Još seljačkije,
Ako je prostor kompletan, tj ako sadrzi sve svoje tačke nagomilavanja, niz je Košijev ako i samo ako je konvergen. [ malada @ 30.10.2005. 13:18 ] @
Npr niz 1/n je kosijev ali on nije konvergentan u metrickom prostoru realnih brojeva bez nule sa d2 metrikom.
[ del-boy @ 30.10.2005. 22:06 ] @
E ovo mi već govori nešto!
Samo, šta je d2 metrički prostor. Nismo ih mnogo učili, a mislim da ovaj nismo pominjali. [ uranium @ 30.10.2005. 23:08 ] @
Mala napomena:
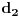 nije metrički prostor nego funkcija pomoću koje merimo rastojanja između tačaka (u ovom konkretnom slučaju skupa nije metrički prostor nego funkcija pomoću koje merimo rastojanja između tačaka (u ovom konkretnom slučaju skupa 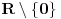 ). ).Uopšte, ako imamo neki neprazan skup 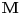 , onda za funkciju , onda za funkciju 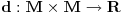 , kažemo da je metrika na , kažemo da je metrika na 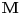 akko za svako akko za svako 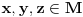 važi: važi:1. 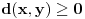 2. 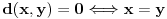 3. 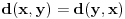 4. 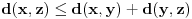 . .Uređeni par 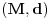 se onda naziva metričkim prostorom, mada se obično kaže samo: metrički prostor se onda naziva metričkim prostorom, mada se obično kaže samo: metrički prostor 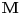 , ako je poznato na koju metriku se misli. , ako je poznato na koju metriku se misli.U primeru koji je dao malada mislilo se na specijalan slučaj sledeće situacije: neka je dat skup 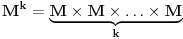 i neka je za proizvoljno realno i neka je za proizvoljno realno 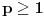 metrika data sa metrika data sa 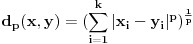 , pri čemu je , pri čemu je 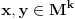 , tj. , tj. 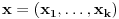 i i 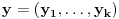 . .Kada uzmemo da je 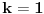 i i 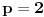 , dobijamo metriku , dobijamo metriku 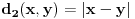 (koju ja volim da zovem "standardna" ili "uobičajena" (koju ja volim da zovem "standardna" ili "uobičajena" [Ovu poruku je menjao uranium dana 31.10.2005. u 00:12 GMT+1] [ del-boy @ 31.10.2005. 10:06 ] @
Hvala na razjašnjenju!
Ove aksiome za metrički sistem sam znao! Jedino što se nisam dobro izrazio kada sam rekao da je d2 metrički prostor. [ zi:: @ 31.10.2005. 10:18 ] @
Citat: peddja_stankovic: Još seljačkije, Ako je prostor kompletan, tj ako sadrzi sve svoje tačke nagomilavanja, niz je Košijev ako i samo ako je konvergen. E, ako ti je ovo seljacki ... probaj ovo pokazati nekom seljaku ... [ peddja_stankovic @ 31.10.2005. 20:26 ] @
[att_img]
Evo jedne moje pesnicke vizije tacke nagomilavanja. U U nekim okolinama zelene i plave tacke se nalazi se beskonacno a u nekim konacno clanova dok u svakoj okolini crvene tacke se nalazi beskonacno mnogo clanova niza. Zato bi crvena trebalo da asocira na tacku nagomilavanja. Ako niz ima jednu tacku nagomilavanja onda se to zove granicna vrednost niza. Rastojanje medju clanovima niza koji teze crvenoj tacki postaje beskonacno mala. To je sustina Kosijevog kriterijuma. Prilicno apstraktno? p.s. robot nije moje delo, to sam nasao na netu. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|