[ iggy91 @ 06.11.2005. 14:29 ] @
| Zna li neko kako se ovo dokazuje? Znam da je 100% moguce, ali ne znam kako..... Ako neko zna mozda neki link do sajta koji ovo objasnjava, nek javi... |
|
[ iggy91 @ 06.11.2005. 14:29 ] @
[ Shadowed @ 06.11.2005. 14:37 ] @
Ne mozes to dokazati. Postoje neki kvazi dokazi ali oni naravno uvek imaju neku zackoljicu zbog koje to nije tacno.
[ Bojan Basic @ 06.11.2005. 14:43 ] @
Ajde razmisli malo šta si napisao. Da li si svestan da, kad bi to bila istina, bi pala kompletna matematika koja do sada postoji? Zapravo, iz postojećeg sistema aksioma se može pokazati da je baš 1+1=2 i ništa drugo.
E sad, ono što si verovatno video ili čuo je da neko da pogrešan dokaz tamo neke gluposti, u kojima se greška najčešće vidi i iz aviona, ali eto - ljudi budu opsednuti time što su "srušili kompletnu matematiku" pa i ne pročitaju kako treba ono što piše. Takvih stvari možeš naći koliko hoćeš, evo npr. ja ću ti "dokazati" da je 1+1=3: 1+1=1+2=3 E sad, otkud nam ovo drugo? Vrlo prosto, sledi iz poznate stvari 1=2 koja je već "dokazana" na ovom forumu, videti http://www.elitesecurity.org/tema/28509. [ dejan_su @ 06.11.2005. 15:35 ] @
16 - 16 = 20 - 20
4 * (4 - 4) = 5 * (4 - 4) Kada se podeli sa (4 - 4) dobije se da je 4 = 5 Eto dokaz ako zaboravimo da nema deljenja sa nulom... [ felixfelix @ 06.11.2005. 19:41 ] @
Bice da si malo zaboravio koje matematicke operacije imaju prednost i sta se prvo radi u matematickim izrazima.
[ zarkomd @ 15.11.2005. 11:11 ] @
Citat: 16 - 16 = 20 - 20 4 * (4 - 4) = 5 * (4 - 4) Kada se podeli sa (4 - 4) dobije se da je 4 = 5 Eto dokaz ako zaboravimo da nema deljenja sa nulom... ne mozes da delis sa (4-4) = 0 [ Sun Tzu @ 15.11.2005. 11:50 ] @
Vrlo jednostavno i matematicki tacno rjesenje je da operaciju + (plus) definišemo kao plus+1 (++1) u "običnoj" matematici. Dakle:
1+1=3 1+2=4 .. 2+5=8 itd. [ dejan_su @ 15.11.2005. 19:17 ] @
Citat: zarkomd: ne mozes da delis sa (4-4) = 0 Pa napisao sam to... [ [email protected] @ 17.11.2005. 18:53 ] @
---------0-1-2-3-4-5-6-7-8-9...---------------........do beskonacnosti naravno ali ima istine izmedju svakog broja je praznina,nekakva pa je ono- neki broj .Elem, 1-+jos jednom - +1 je 3-....Razmisli
[Ovu poruku je menjao [email protected] dana 18.11.2005. u 23:46 GMT+1] [ 3MAJ86 @ 18.11.2005. 22:28 ] @
pa to nije tačno, jer se skup prirodnih brojeva (istovremeno i celih) ne definiše na taj način. tako da ti nemaš izmedju brojeva te ''praznine'' i ''-'' nikako ne može da bude broj (bar ne u tom skupu)
[ [email protected] @ 18.11.2005. 22:45 ] @
bas i nije tako ali ne zelim da diskutujem o tome kad vidim da za tebe nema niceg u beskonacnom nizu brojeva osim da su celi,prosti...tupi,zamorni,smaraju,bez tona,slike to je tvoj alg. izraz.Ne ni ovaj svijet nije celina a da izmedju ostalog ne prodje po koja kometa...Zamisli brojeve tako.Ako me razumijes.C-C-C
[ 3MAJ86 @ 20.11.2005. 17:09 ] @
nisu meni brojevi tako "tupi, prosti i beskonachni..." kao shto kazhesh, ali jednostavno ne zhelim da izmishljam sam neku svoju matematiku.
mislim glupo je matematicharima prichati kako je matematika najegzaktnija nauka, i jednostavno je kao takvu poshtujem i drzhim se njenih pravila i definicija. shvatam shta zhelish da kazhesh, ali se jednostavno ne slazhem sa time. [ petarm @ 08.12.2005. 14:12 ] @
1.) Dokazati da je 1+1=3 za dovoljno veliko 1. Mislim da je na to mislio.
[ Reynolds @ 18.12.2005. 20:40 ] @
Svi su brojevi isti!
uzmimo da je a + b = c tada je to drukčije napisano 3a - 2a + 3b - 2b = 3c - 2c ako to malo sredimo 3a + 3b - 3c = 2a + 2b - 2c izlučimo 3(a + b - c) = 2(a + b - c) podijelimo sa (a + b - c) i dobivamo 3=2 :D A 1+1 = 3 za iznimno visoke vrijednosti broja jedan :) [ dejan.djuric @ 18.12.2005. 20:55 ] @
Citat: Reynolds: Svi su brojevi isti! uzmimo da je a + b = c tada je to drukčije napisano 3a - 2a + 3b - 2b = 3c - 2c ako to malo sredimo 3a + 3b - 3c = 2a + 2b - 2c izlučimo 3(a + b - c) = 2(a + b - c) podijelimo sa (a + b - c) i dobivamo 3=2 :D A 1+1 = 3 za iznimno visoke vrijednosti broja jedan :) ...još samo da je a+b-c <> 0 i bilo bi super.... [ Reynolds @ 19.12.2005. 20:09 ] @
Citat: dejan.djuric: ...još samo da je a+b-c <> 0 i bilo bi super.... ... i još da se u dokazu smije postupati kao u jednadžbi, odn. prebacivati s strane na stranu :) ... [ Bojan Basic @ 19.12.2005. 20:18 ] @
Naravno da sme da se prebacuje, zašto ne bi smelo?
[ Farenhajt @ 21.12.2005. 18:49 ] @
Vrlo prosto: 1+1=3 je, štaviše, aksiom ukoliko se dogovorimo da umesto 2 pišemo 3...
U takvim slučajevima "pretumbacije" brojeva svakakve zanimljive jednakosti i osobine mogu da iskrsnu: 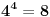 , , 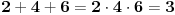 , ,  , , 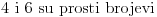 , , 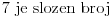 - ALI s druge strane - ALI s druge strane 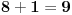 , , 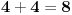 i i  ... (sve to ukoliko se npr. dogovorimo da "normalan" poredak cifara glasi 0, 2, 4, 6, 8, 1, 3, 5, 7, 9). ... (sve to ukoliko se npr. dogovorimo da "normalan" poredak cifara glasi 0, 2, 4, 6, 8, 1, 3, 5, 7, 9).[Ovu poruku je menjao Farenhajt dana 21.12.2005. u 19:53 GMT+1] [ zarkomd @ 19.01.2006. 19:59 ] @
i mozes da drugacije definises operaciju + .
[ braker @ 20.01.2006. 23:20 ] @
Citat: Ja bih se samo prisetio Rusell-a i njegove filozofije matematike,gde su brojevi oznaceni kao komparativna pomagala.Uzmimo skup koji ima(slovima) DVA elementa, za simbol za DVA uzmimo 3.Znaci,imamo skup koji broji(slovima)-DVA,(simbolima)-3 elementa.Ovako ja shvatam relativnost usvojenog brojnog sistema. Parafraza iz istoimene knjige-Ako bi chovek bio u stanju da svoje razmishljanje predstavi matematichkim SIMBOLIMA(nikako brojevima :):)),uz korishtenje elementarnih zakona logike,svakako bi bio oslobodjen lutanja u neznanju i neodredjenosti. [ thePOET @ 25.01.2006. 16:29 ] @
Da se ubacim, ali malo prekasno :)
Imas dva konopca sa po jednim cvorom na sebi. kada ta dva konopca vezes jedan za drugi dobijes konopac sa tri cvora. Eto, 1 + 1 = 3. (By the way, znam da je ovo isto kao i onaj post sa ++, ali ovako je simpaticnije :) ) p0z [ profilic @ 04.05.2006. 13:19 ] @
Ako nisam isuvise zakasnio evo kako se to moze i pomocu digitrona, odnosno racunara. Naime u excelu upises broj 1,4999999999999999... i saberes ga sa istim takvim i dobices 3. Da bi bilo da je 1+1=3 onda odes na format cells i upises broj decimala=0. Tako ces videti da je 1+1=3 :). Naravno mozes da upises i sve brojeve koji su veci od 1,25 i manji od 1,5 (mogu biti isti i razliciti).
Pozdrav [ jorganwd @ 09.05.2006. 15:20 ] @
"I tako je počeo njegov novi život. Prao je čarape snegom, pio čaj od snega i čistio sneg tako da je do kraja zime proglašen za najboljeg u smeni. Budio se sa otiscima uha u peškiru mokrom od suza i bale, koji mu je služio umesto uzglavlja i besomučno je čistio sneg. Sledeće zime o njemu su pisale mesne novine, a kroz dve godine pojavi se u prestoničkoj "Pravdi" beleška o njegovim uspesima. Postao je najbolji čistač snega u o kugu i jedan od najboljih u čitavoj zemlji. Ponekad je uveče sanjao dvanaest brodova pod imenima dvanaest apostola, ili trinaest konjanika što nose raspeće i baldahin, pokušavajući da u trku stignu četrnaestog konjanika. Kada ga uhvatiše u senku baldahina stadoše.
— Ko si ti? — upitali su ga Hristovi učenici okupljeni oko raspeća, onako iz sedla. — Ja sam četrnaesti učenik — uzvratio je nepoznati ispod baldahina i Razin se probudio. Lice mu je bilo puno nekakvog peska, protrljao ga je i zaključio da su to osušene suze iz snova. Plakao je u snu za svojim sinom kojeg nikada nije video, iako ga je imao. Očigledno, još uvek snovi i suze dolazili su iz njegovog bivšeg života, kasnili su. A potom je ustao i hteo da se lati lopate. Ali, tog jutra nisu mu je dali. Zadržali su ga u baraci. Došao je da ga vidi jedan mlad čovek. Krajevi obrva i brkova pažljivo su mu bili zavučeni pod šal kojim je uvijao glavu. Njegov pogled pade po licu Fjodora Aleksejeviča kao prašina, mladić skide jednoprstu rukavicu i u ruci mu se pojavi upaljena cigareta. Stavio je cigaretu u usta, izvadio nož oštren za levaka i komad slanine, odsekao levom rukom parče, pružio ga Fjodoru Aleksejeviču i odmah prešao na stvar. Ugled najboljeg radnika koji uživa Aleksej Fjodorovič (tako se Razin prijavio u svom novom mestu i tako su ga zvali) obavezuje sve, pa i samog Alekseja Fjodoroviča. Treba zato da uđe u komunističku partiju. I to neodložno. To bi imalo veoma dobar odjek i izvan mesta, šire gledano... Razin se sledio kada je čuo ovaj predlog i mozak mu je počeo raditi brzo, ali on ču kako se u prozor zakašlja vetar, pa odustavši od razmišljanja reče: — Ali, dragi druže, pa ja sam nepismen, kako mogu biti takav u partiji? — Ništa zato, Alekseju Fjodoroviču, ništa. Imamo mi još takvih kao što si ti. Natalija Filipovna Skargina njima lepo slovca pokazuje, tečaj za nepismene vodi i vas ćemo tamo sa ostalim bezgramotnima, pa kad izučite, počećete i na sastanke dolaziti, a dotle jedno mesec dana nećemo te uznemiravati. I tako Fjodor Aleksejevič ode Nataliji Filipovnoj. Našao se u lepoj drvenoj zgradi, u hodniku zatekao gomilu lopata i 24 para čizama. Izuo se i sam i ušao u neverovatno nisku odaju punu skamija. U njima su sedela 24 polaznika kursa Natalije Filipovne, pušili su se onako mokri, grizli krajeve olovaka i pisali po diktatu same Skargine slovo i: kosa tanka, uspravna debela... Peć je pocupkivala u uglu i prosipala vodu pristavljenu za čaj, Natalija Filipovna je sedela iza stola i obratila se radosno novodošavšem, koji je grbinom odirao tavanicu: — Poginješ, poginješ glavicu! Tako i treba pred nastavnicom. Zato se odvajkada niska, što niža tavanica udara, da se ne kočoperite. I posadila je Fjodora Aleksejeviča, ponudila ga čajem, pri čemu se videlo da je Natalija Filipovna Skargina u stvari stajala iza svog stola i da je takvoga rasta da izgleda kad sedi kao da stoji. Potom se okrenula tabli, iz uha izvukla komadić krede i počela čas matematike. — Jedan plus jedan — pisala je i naglas sricala Natalija Filipovna — jedan plus jedan jesu dva! I to i u ponedeljak i u utornik, upamtite. I juče su bili i biće vo vjek i vjekov dva i samo dva. U sobi je bilo toplo, peć je počela da šeta ko puštena s lanca, svi su sricali: jedan plus jedan jesu dva, Fjodor Aleksejevič i sam je uzeo plajvaz da pribeleži ono sa table i tada ne izdrža. On tek sada shvati da se, otkad je uzeo lopatu da čisti sneg, ne znoji više i da sve to neisceđeno mora nekud iz njega napolje. I prvi put za sve ove godine ne izdrža. Ustao je odlučno, odmah udario glavom o tavanicu, izišao na tablu, obratio se svojim predašnjim samouverenim glasom Nataliji Filipovnoj koja je nemo gledala u njega i rekao na zaprepašćenje svih prisutnih: — To je matematika XIX stoleća, draga Natalija Filipovna. Dozvolite da to primetim. Današnja, moderna matematika drugačije gleda na stvari. Ona zna da jedan i jedan ne moraju uvek biti dva. Dajte mi tu kredu za časak, pa ću vam odmah dokazati. I Fjodor Aleksejevič je počeo urođenom brzinom ispisivati po tabli brojeve. Jednačina za jednačinom se redala, u prostoriji je vladao tajac, profesor je prvi put posle toliko godina ponovo radio svoj posao, doduše, onako pognut nije imao najbolji pregled brojki, kreda je čudno nekako škripala i odjednom rezultat je ispao sasvim protiv očekivanja Fjodora Aleksejeviča opet 1+1=2. — Trenutak! — uzviknuo je Fjodor Aleksejevič — nešto nije u redu, samo trenutak, odmah ćemo videti gde je greška — a po glavi mu se motala besmislica: Sve izgubljene partije karata čine celinu! i od nje nije mogao da računa. Misli su grmele u njemu i grmljavina misli zaglušivala je sve ostalo. Ali, njegova besprimerna umešnost išla mu je naruku, on je odmah znao gde će naći omašku i poleteo kredom po redovima ispisanih brojeva, sa kojih se već krunio beli prah. I u tom času ceo razred, njih dvadeset četvorica, svi sem Natalije Filipovne Skargine, počeli su uglas da mu šapuću rešenje: — Plankova konstanta! Plankova konstanta!" Odlomak iz knjige 'Predeo slikan cajem' :) [ klichko @ 09.05.2006. 17:50 ] @
Mi smo u srednjoj koristili ovo:
Code: pretpostavimo da je a = b (npr. a=2=1+1, b=3) a - (a+b)/2 = b - (a+b)/2 /^2 a^2 - a(a+b) + ((a+b)/2)^2 = b^2 - b(a+b) + ((a+b)/2)^2 a^2 - a^2 - ab = b^2^ - b^2 - ab ab = ab tj. a = a ^ b = b Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|