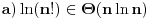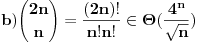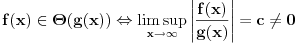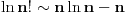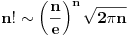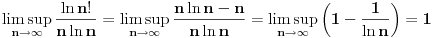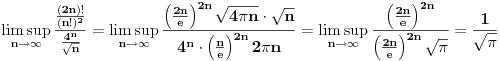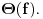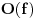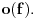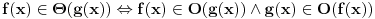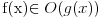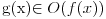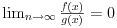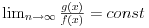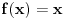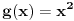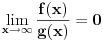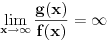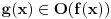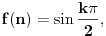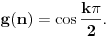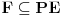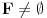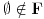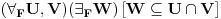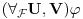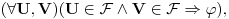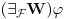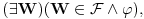[ amel @ 11.11.2005. 15:10 ] @
|
[ Bojan Basic @ 11.11.2005. 15:53 ] @
[ amel @ 11.11.2005. 16:28 ] @
Bojane, puno se zahvaljujem na ovako efikasnom i brzom odgovoru, samo ja to moram malo razraditi da skontam o cemu se radi i na koji nacin
Puno pozdrava i zahvaljujem jos jednom Amel [ Nedeljko @ 16.11.2005. 18:18 ] @
[ Bojan Basic @ 16.11.2005. 18:24 ] @
[ Bojan Basic @ 16.11.2005. 20:57 ] @
[ peddja_stankovic @ 16.11.2005. 21:36 ] @
Vidim da sam bio u suptilnoj zabludi. Ne znam odakle mi to.
Ovde je lepo objasnjeno. http://en.wikipedia.org/wiki/B....2C_.CF.89.2C_.CE.98.2C_.C3.95 [ Nedeljko @ 16.11.2005. 23:21 ] @
Relacija
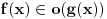 se može još zapisivati kao se može još zapisivati kao 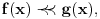 i čita se "f(x) je zanemarljivo u odnosu na g(x)". Relacija i čita se "f(x) je zanemarljivo u odnosu na g(x)". Relacija 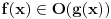 se može zapisivati kao se može zapisivati kao 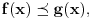 (doduše sa iskrivljenom crtom ispod (doduše sa iskrivljenom crtom ispod 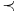 ) i čita se "f(x) je podređeno u donosu na g(x)". Relacija ) i čita se "f(x) je podređeno u donosu na g(x)". Relacija 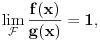 gde je gde je 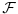 bazis filtra koji opisuje granični proces, se može zapisivati kao bazis filtra koji opisuje granični proces, se može zapisivati kao 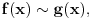 i čitati kao "f(x) je asimptotski ekvivalentno sa g(x)". Relacija i čitati kao "f(x) je asimptotski ekvivalentno sa g(x)". Relacija 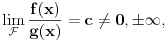 gde je gde je 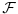 bazis filtra koji opisuje granični proces, se može zapisivati kao bazis filtra koji opisuje granični proces, se može zapisivati kao 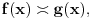 i čitati kao "f(x) je asimptotski slično sa g(x)". i čitati kao "f(x) je asimptotski slično sa g(x)".[ amel @ 17.11.2005. 14:46 ] @
Sve je to ok, taman sam mislio da sam skonto medjutim, kako cu onda dokazati
da je 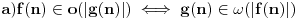 b) Dati funkciju f,g za koju vrijedi 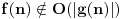 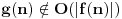 c)Ako postoji 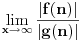 onda slijedi onda slijedi 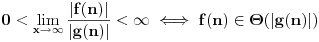 Nasao sam materijala o ovome, medjutim problem je kako dokazati ove navedene stvari? To bi mi trebalo do veceras. Dogurao sam donekle, medjutim nije to to sto ja mislim. Unaprijed hvala [ Nedeljko @ 17.11.2005. 21:59 ] @
[ karas @ 18.11.2005. 08:20 ] @
Nedeljko, može kratko objašnjenje šta je bazis filtra? Čuo sam od nekih starijih kolega da je Arandjelović (ako sam mu dobro zapamtio ime) to koristio ali nikada nisam naleteo na taj pojam.
[ uranium @ 18.11.2005. 16:29 ] @
[ karas @ 20.11.2005. 11:08 ] @
Meni ovo liči na jednu od Hauzdorfovih aksioma za topološki prostor, ako ih se dobro sećam. Ne znam koliko je dobro uvoditi bazis filtru za izlaganje analize I.
[ Nedeljko @ 21.11.2005. 08:25 ] @
[ karas @ 21.11.2005. 11:31 ] @
Nisam sumnjao u tačnost, ali me je podsetilo na one T1-T4 aksiome za Hauzdorfove prostore. Hvala na objašnjenju.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|