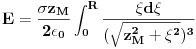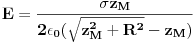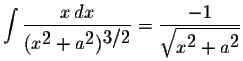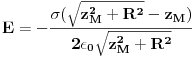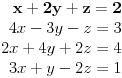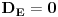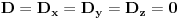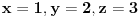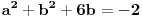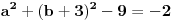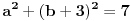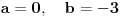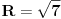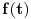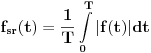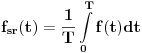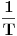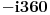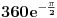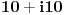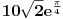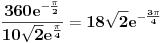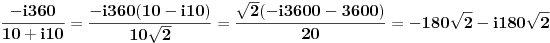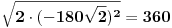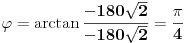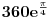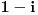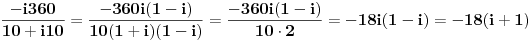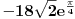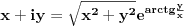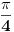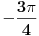|
|
[ srki @ 21.11.2005. 03:42 ] @
Mislim da je lakse da ti ostavis postupak pa da ti kazemo gde je greska.
[ milanche @ 21.11.2005. 05:11 ] @
Probaj sa sledecom smenom promenljivih:
x^2 + a^2 = U; dU = 2xdx
cime se integral svodi na integral stepene funkcije
1/2*integral(u^(-3/2)du),
koji je tablicni slucaj, a resenje je razlomak - u brojiocu je x^(-3/2 + 1) a u
imeniocu (-3/2 + 1).
Kad se sve lepo sredi, dobijes ocas posla bas to sto kazu na tom tvom sajtu.
[ R A V E N @ 03.02.2006. 18:38 ] @
Pa hvala ti,milanche,svakako ću proučiti to što si naveo.A sada ako može nečiji komentar na slijedeći problem:
Dat je sistem čiju saglasnost treba ispitati i u slučaju saglasnosti riješiti ga:
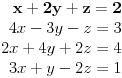
Ovakav sistem se rješava pomoću eliminante,za koju sam utvrdio da je jedanka nuli,tj. 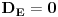 .Prema tome sistem je saglasan i može se riješiti,zar ne?
Sada sam izdvojio prve tri jednačine sistema i rješavao ih nezavisno,jer će njihovo rješenje zadovoljiti i četvrtu jednačinu.Utvrdio sam za taj tročlani sistem da je 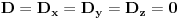 .
U Zbirci iz matematike od Branislava Stojanovića(Svjetlost Sarajevo,1981.) sam našao da se u ovom slučaju sistem nastavlja rješavati tako što se izračunaju subdeterminante sistema koje se se formiraju iz elemenata determinante  sistema.
Za te subdeterminante sam našao da nisu sve jednake nuli i za takav sistem piše:
"Ako je bar jedna od subdeterminanata determinante sistema različita od nule,onda je takav sistem neodređen i ima beskonačno mnogo rješenja,a za jednačine kažemo da su zavisne."
No,ako ja npr. uvrstim proizvoljne nepoznate kao što su 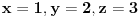 ,one ne odgovaraju jednačinama,pa me interesuje komentar na ovaj moj postupak i moguća uputa.Žao mi je ako je zadatak(ovaj ili neki budući)suviše trivijalan,a čisto "fizički" posao oko računanja znam i sam.Hvala unaprijed!  [Ovu poruku je menjao R A V E N dana 04.02.2006. u 21:13 GMT+1]
[Ovu poruku je menjao R A V E N dana 04.02.2006. u 21:13 GMT+1][ peddja_stankovic @ 04.02.2006. 07:39 ] @
Pogresio si sto si uzeo prve pri jednacine. Ako uzmes prvu, drugu i cetvrtu dobices resenje 1 0 1 za x y i z.
Treca jednacina je isto sto i prva samo pomnozena sa 2.
Inace ovo se radi malo drugacije i sistematicnije ali bi potrajalo pisanje algoritma.
Drugo, da je sistem stvarno imao beskonacno mnogo resenja to ne znaci da su i sve kombinacije x, y i z-ova resenja
Na primer
x+y=1
x+y=1
ima beskonacno mnogo resenja i resenja su oblika
x=t
y=1-t
gdenje t proizvoljan realni broj. Na primer za t=5 dobija se x=5 i y=-4. Lako se provarava da ovaj par zadovoljava obe jednacine sistema dok x=1 i y=1 ne zadovoljava sistem.
[ R A V E N @ 05.02.2006. 17:10 ] @
U redu.A je li postoji neko pravilo na koje mogu da se oslonim kad vršim odabir jednačina,tako da dobijem zbilja rješenja,a i da pravilno zaključim kad je sistem zbilja neodređen sa beskonačnim brojem rješenja?
Kad kažeš "sistematičnije",vjerovatno misliš na metodu upoređivanja ranga matrice sistema i ranga proširene matrice sistema,što mi je predložio i E N I A C,član ovog foruma. 
Pretpostavljam da se svi neodređeni sistemi sa beskonačno mnogo rješenja "sređuju" na taj način što se jedna nepoznata izjednači sa parametrom  i preko nje određuju ostale nepoznate sistema?
[Ovu poruku je menjao R A V E N dana 05.02.2006. u 18:10 GMT+1][ peddja_stankovic @ 05.02.2006. 19:41 ] @
Ovako ode Gausov algoritam:
Prvi red pomnozis sa -4 i dodas drugom redu
onda prvi pomnozis sa -2 i dodas trecem
onda prvi pomnozis sa -3 i dodas cetvrtom
[ 1 2 1 | 2]
[ 4 -3 -1 | 3]
[ 2 4 2 | 4]
[ 3 1 -2 | 1]
Dobijes
[ 1 2 1 | 2]
[ 0 -11 -5 | -5]
[ 0 0 0 | 0]
[ 0 -5 -5 | -5]
Prvi i drugi red prepises pa pomnozis drugi red sa -5 a cetvrti sa 11 i saberes na
mestu cetvrtog reda
[ 1 2 1 | 2]
[ 0 -11 -5 | -5]
[ 0 0 0 | 0]
[ 0 -5 -5 | -5]
Dobijes
[ 1 2 1 | 2]
[ 0 -11 -5 | -5]
[ 0 0 0 | 0 ]
[ 0 0 -30 | -30]
Treci red otpada
[ 1 2 1 | 2]
[ 0 -11 -5 | -5]
[ 0 0 -30 | -30]
rang(A)=3 i rang(A')=3 sledi da ima resenja
Resenje lako sledi 1 0 1
[ R A V E N @ 19.08.2006. 22:38 ] @
Citat: milanche: Probaj sa sledecom smenom promenljivih:
x^2 + a^2 = U; dU = 2xdx
cime se integral svodi na integral stepene funkcije
1/2*integral(u^(-3/2)du),
koji je tablicni slucaj, a resenje je razlomak - u brojiocu je x^(-3/2 + 1) a u
imeniocu (-3/2 + 1).
Kad se sve lepo sredi, dobijes ocas posla bas to sto kazu na tom tvom sajtu.
Provjerio sam,i sa smjenom se dobije isti rezultat.Vjerovatno je po srijedi krupna štamparska greška. [ R A V E N @ 12.04.2007. 22:13 ] @
Evo jedan koji nije baš iz ove oblasti ali nema potrebe da otvaram novu temu:
Odrediti geometrijsko značenje izraza: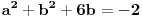
E sad,koliko sam shvatio u zadatku se pita: Kakvu sliku predstavlja ova jednačina u koordinatnoj ravni?Prilično sam siguran da je ovo kružnica,no kako pokazati da je kružnica?Koje su koordinate centra te kružnice? [ Daniel011 @ 12.04.2007. 22:35 ] @
[ R A V E N @ 12.04.2007. 22:49 ] @
Yeah,hvala ti Daniel011!
Uštedio si mi napor detaljnog traženja po zbirkama/matematikama.
[ R A V E N @ 23.09.2007. 21:24 ] @
Je li vidi iko kako pojednostaviti ovu gigantsku determinantu,ako je to uopće moguće.Pod "pojednostaviti" mislim da se u jednom redu ili koloni dobije još dodatnih nula dodavanjem nekog drugog reda ili kolone pomnoženog(e) nekim brojem:

Kako god da krenem,uvijek u nekom redu ili koloni kada uklonim jednu nulu dobijem i jednu "ne-nultu" vrijednost.
Stvar je da je ovo determinanta sistema od 6 jednačina i ovo su koeficijenti uz nepoznate koje predstavljaju naelektrisanja kondenzatora jednog elektrostatičkog kola,a vidim da je rješavanje ove determinante "pješke" prilično tricky job.Metoda rješavanje koja je primjenjena su Kirhofovi zakoni.
[Ovu poruku je menjao R A V E N dana 24.09.2007. u 00:10 GMT+1][ R A V E N @ 13.04.2008. 19:04 ] @
Koja je tačna formula za srednju vrijednost periodične funkcije 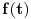 na njenom periodu  :
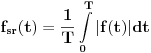 ili 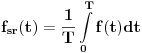 ?
Nekako mi djeluje da je druga,jer uzima u obzir i negativne vrijednosti koje funkcija može imati tokom tog perioda.
edit:korekcija na Daniel011-ovu primjedbu
[Ovu poruku je menjao R A V E N dana 14.04.2008. u 20:33 GMT+1][ Daniel011 @ 13.04.2008. 20:29 ] @
Ispred integrala treba da stoji 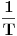 , da bi se radilo o srednjoj vrednosti.
A koji će izraz biti tačan, upravo i zavisi od toga da li se traži srednja apsolutna vrednost funkcije, ili srednja vrednost funkcije.
Primera radi, srednja vrednost sinusne ili kosinusne funkcije je nula. Ali ako se traži recimo srednja udaljenost od ravnotežnog položaja kod mehaničkih oscilacija, onda će se posmatrati srednja apsolutna vrednost sinusne (kosinusne) funkcije. [ R A V E N @ 03.06.2008. 21:58 ] @
Ako uzmem kompleksni broj 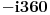 te ga pretvorim u Eulerov oblik kompleksnog broja,dobivam 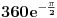 .
Sada to isto uradim i sa kompleksnim brojem 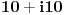 te dobijem 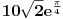 .
Podijelim li ta dva broja u njihovom Eulerovom obliku,dobivam:
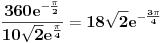 .
Međutim,ako izvršim njihovo dijeljenje u algebarskom obliku,dobivam:
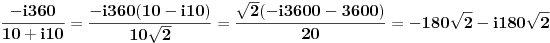 .
Sada,ako pretvorim ovaj rezultat u Eulerov oblik,dobivam:
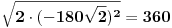
i
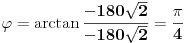 .
Očigledno je da rezultat 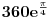 ne odgovara onom dobivenom u dijeljenju preko Eulerovog oblika.U čemu griješim?
[Ovu poruku je menjao R A V E N dana 03.06.2008. u 23:14 GMT+1][ Kolins Balaban @ 03.06.2008. 22:21 ] @
onako na brzinu, samo primjetio sljedece:
kod dijeljenja algebarskih oblika kompl brojeva, sto i brojnik i nazivnik nisi pomnozio samo sa 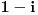 ?
imao bi sljedece:
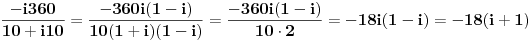
a to bi trebalo da bude
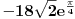 [ R A V E N @ 04.06.2008. 00:00 ] @
A u čemu je moja greška?  [Ovu poruku je menjao R A V E N dana 04.06.2008. u 01:10 GMT+1]
[Ovu poruku je menjao R A V E N dana 04.06.2008. u 01:10 GMT+1][ Kolins Balaban @ 04.06.2008. 00:09 ] @
jest ti postupak ok, ali imas gresku u nazivniku, odmah poslije prve jednakosti. ne mozes dobiti nikako 10 korjena iz 2. ne znam otkud ti taj korijen iz 2. trebas dobiti 200 u nazivniku
[ R A V E N @ 04.06.2008. 00:12 ] @
Da,da,jasno je,hvala!Moja omaška.Ja sam krenuo da korjenujem gdje ne treba.
Možeš li pogledati ovaj moj post? [ cicika @ 04.06.2008. 11:28 ] @
Raven, pogledaj na trigonometrijskom krugu za taj arkustangens gde ti se nalaze x i y... videćeš da su oni negativni pa se tvoj ugao nalazi u trećem a ne u prvom kvadrantu. I iznosi -3pi/4.
[ cicika @ 04.06.2008. 11:35 ] @
Citat: ne mozes dobiti nikako 10 korjena iz 2. 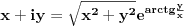
Odatle... [ R A V E N @ 04.06.2008. 14:38 ] @
Citat: cicika: Raven, pogledaj na trigonometrijskom krugu za taj arkustangens gde ti se nalaze x i y... videćeš da su oni negativni pa se tvoj ugao nalazi u trećem a ne u prvom kvadrantu. I iznosi -3pi/4.
Eh,to,to,a ja baš krenuh napisati da imam problema sa dobivanjem tačnog argumenta,naime dobivao sam 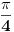 tamo gdje sam trebao 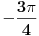 .  Odsada obavezno skica trigonometrijske kružnice uz svaki zadatak. 
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|