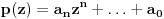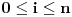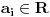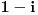[ ona_ @ 23.11.2005. 12:19 ] @
| naci a, b iz R, tako da (1 + i) prestavlja resenje jednacine: z^3 + z^2 + (a + 2i) . z + 7 + ib = 2i da li mogu da z zamenim sa (1 + i)? kada tako uradim, dolazim do: a = -3, b = -1. ako ne mogu, kako da postavim? moze li mi neko pomoci? |