[ Tilia @ 23.11.2005. 20:30 ] @
| Večer! Zna li tko koja je najčešća praktična primjena verižnih razlomaka? I kako se na engleskom kaže 'verižni'? Literature skoro da i ne nadjem, pa pliz ostavite kakav koristan link vezan uz ovu temu. Tnx svima! |
|
[ Tilia @ 23.11.2005. 20:30 ] @
[ Bojan Basic @ 23.11.2005. 20:48 ] @
Ne engleskom se kaže continued fraction, a jedna od primena već diskutovana na ovom forumu je rešavanje Pelove jednačine.
[ Nedeljko @ 23.11.2005. 23:08 ] @
Najvažnija osobina verižnih razlomaka je da oni predstavljaju najbolje racionalne aproksimacije brojeva.
Za svaki realan broj  i prirodan broj i prirodan broj  postoji tačno jedan ceo broj postoji tačno jedan ceo broj  takav da važi takav da važi 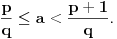 Time si našao jednu gornju i jednu donju procenu tog broja od kojih niti jedna ne odstupa od datog broja Time si našao jednu gornju i jednu donju procenu tog broja od kojih niti jedna ne odstupa od datog broja  za više od za više od 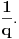 Međutim, može se desiti da postoji prirodan broj Međutim, može se desiti da postoji prirodan broj 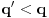 takav da za neki prirodan broj takav da za neki prirodan broj 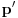 važi da je aproksimacija važi da je aproksimacija 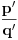 bliža broju bliža broju  nego bilo koji od brojeva nego bilo koji od brojeva  Cilj je naći što bližu racionalnu aproksimaciju datog broja, ali sa što manjim imeniocem. Cilj je naći što bližu racionalnu aproksimaciju datog broja, ali sa što manjim imeniocem.Aproksimacija 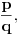 gde je gde je  ceo a ceo a  prirodan broj, broja prirodan broj, broja  je najbolja racionalna aproksimacija tog broja ako je je najbolja racionalna aproksimacija tog broja ako je 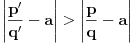 za sve cele brojeva za sve cele brojeva 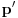 i prirodne brojeve i prirodne brojeve 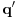 za koje je za koje je 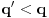 ili ili  i i  Svaki iracionalan broj ima beskonačno mnogo najboljih aproksimacija. Sve njegove verižne aproksimacije su najbolje, ali postoje i primeri najboljih racionalnih aproksimacija iracionalnih brojeva koje se ne dobijaju iz njegovog verižnog razvoja. Dakle, verižni razlomci su se koristili za pronalaženje što boljih aproksimacija iracionalnih brojeva, ali tako da budemo ekonomični sa imeniocem. [ Reynolds @ 18.12.2005. 23:04 ] @
Još jedna primjena verižnih razlomaka nalazi se u dobivanju iznosa zlatnog reza - Phi iz Fibonaccijevih brojeva.
Npr...  Ukoliko se takav raspis nastavi, dobiva se;  Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|