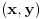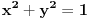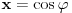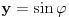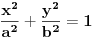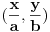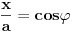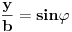[ 04sale82 @ 29.11.2005. 09:41 ] @
| Parametarske jednačine elipse gde se x i y izražavaju u polarnom koordinatnom sistemu čija se osa poklapa sa x-osom a centar sa koordinatnim početkom glase: x=a*cos(fi) y=b*sin(fi) Da li neko može da mi objasni i dokaže, pošto meni nije jasno odakle se vidi taj identitet. Hvala ! |