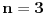
Evo rešenja za (lagano je, a i verovatno nema mnogo veze sa opštim postupkom, pa nikome neću pokvariti užitak...).

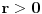
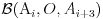
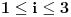
Izaberemo proizvoljnu tačku u ravni i proizvoljan realan broj . Konstruišemo pravilan šestougao, poluprečnika , sa centrom u . Neka su susedna temena označena sa , tako da je: , . Spojimo svako od njih sa tačkom i dobili smo 6 jednakostraničnih trouglova.

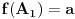
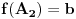
Neka je , i .
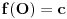
Na osnovu uslova zadatka, dobijamo da mora biti:





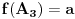
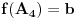
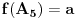
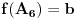
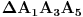
E sad, lako je videti da je jednakostraničan trougao, pa sledi:
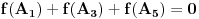
tj. .

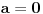
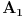
Iz proizvoljnosti tačke sledi tvrđenje.

Da pokušam sada opšti slučaj.

Neka je u ravni dat proizvoljan pravilan -ugao : . Generisaćemo pomoću njega još pravilnih -uglova i dokazati da je .

Za svako fiksirano , rotirajmo tačku oko tačke za svaki od uglova , . Označimo sa sliku tačke pri rotaciji za ugao .Time smo dobili pravilneuglove (svestan sam da je prvi navedeni poligon u stvari samo jedna tačka):







Iz uslova zadatka sada sledi da je:






Uočimo još neke pravilne -uglove:






Iz uslova zadatka sledi:






Pa ako saberemo poslednji niz jednakosti imaćemo:

ali iz prvog niza jednakosti sledi da je svaka od unutrašnjih suma jednaka 0, pa smo dobili da je .

To je to, bravo.