bar neko

Ja sam nešto kao razmišljao još kad si postavio temu, ali nisam uspeo da nađem elementarno rešenje.

Ukratko, nadam se da me nećeš pogrešno razumeti, ali preporučujem ti da naučiš dobro da rešavaš geometrijske zadatke čistom trigonometrijom i/ili kompleksnim brojevima. To ne bi trebalo da bude teško, štaviše usuđujem se da kažem da je dovoljno da uradiš 5-6 zadataka trigonometrijom i 5-6 kompleksnim brojevima (čak može da se radi i o istim zadacima). Ubuduće razmišljaš 15 minuta i ako je elementarno rešenje očigledno onda to i uradiš, a ako nije pređeš na tešku artiljeriju.

Pokusavao sam preko kompleksnih (ako uzmem ABC za jednicni onda imam jos onaj drugi krug pa se mnoooogoo zakomplikuje) . A trigonometrijom isto ne uspevam nista, a da se ne ubijem od racuna. Mislim da je ovde najlakse elementarno .

_{[Ovu poruku je menjao qzqzqz dana 16.12.2005. u 20:41 GMT+1]}

Nažalost, nemam trenutno nikakav program za crtanje geometrijskih slika (preporuke? adrese? hvala unapred ), pa vas molim da uložite mentalni napor pri praćenju dokaza.

Lema 1: Ako je osnovica jednakokrakog trougla a, a odgovarajuća visina h, onda je odstojanje ortocentra od osnovice .

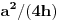
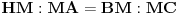
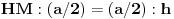
Dokaz preko sličnosti. Neka je C teme, AB osnovica, CM visina i H ortocentar jednakokrakog trougla. Tada su trouglovi AMH i CMB slični (pravougli kojima odgovarajući uglovi imaju normalne krake), te je tj. , odakle je

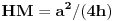
Lema 2: Visina na hipotenuzu pravouglog trougla čije su katete a i b, a hipotenuza c iznosi .

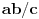
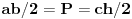
Dokaz elementaran, pošto je , gde je P površina trougla.

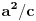
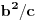
Lema 3: Podnožje visine na hipotenuzu pravouglog trougla čije su katete a i b, a hipotenuza c deli hipotenuzu na delove dužine (uz katetu a) i (uz katetu b).

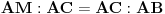
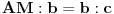
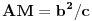
Dokaz takođe prost, primenom sličnosti. Ako je AB hipotenuza, a CM visina pravouglog trougla, onda su trouglovi ABC i AMC slični (zajednički ugao), pa se ima tj. , odakle je . Slično je i .

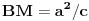
Dokaz glavnog tvrđenja. Neka je AS visina trougla ABC (time je S i centar kružnice k), neka je Q druga presečna tačka kružnice k i duži AF, i neka se duži EQ i PF seku u tački T. Dokazaćemo da su tačke M, T i N kolinearne, iz čega će, zbog simetrije, slediti da je T središte duži MN.

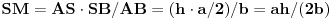
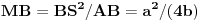
Neka je AB = AC = b, BC = a, AS = h. Pošto je SM hipotenuzna visina trougla ASB (AB je tangenta, a SM poluprečnik kružnice k, pa je ugao BMS prav), prema Lemi 2 imamo da je , a prema Lemi 3 je . Neka je MK visina pravouglog trougla MBS. Prema Lemi 2 imamo da je .

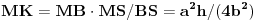
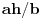
Nadalje, trougao AEF je jednakokrak (AE = AF, što se lako dokazuje preko podudarnosti trouglova ASE i ASF), a T je ortocentar tog trougla, jer su uglovi EPF i EQF pravi, kao uglovi nad prečnikom EF. Pošto je SM = SE = SF (poluprečnici), sledi da je EF = 2SM = , pa je prema Lemi 1

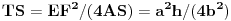
Pošto je TS = MK, dokazali smo da su tačke M, T i N podjednako udaljene od osnovice BC, te su stoga kolinearne, pa je T središte duži MN.

_{[Ovu poruku je menjao Farenhajt dana 20.12.2005. u 19:50 GMT+1]}