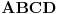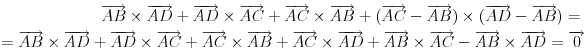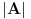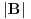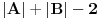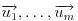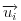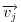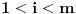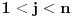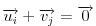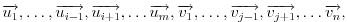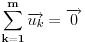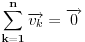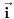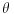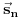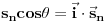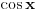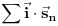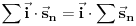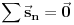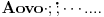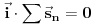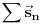|
|
[ Bojan Basic @ 03.12.2005. 19:49 ] @
|
| Rešenje ovog zadatka zauzima dve rečenice i jedno je od najoriginalnijih (i najneobičnijih) rešenja koje sam ja ikada video. Iako formulacija izgleda komplikovano, rešenje je izuzetno jednostavno. Mislim i da je zadatak dosta poznat, ali nema veze.
Svakoj strani poliedra pridružimo vektor normalan na nju usmeren ka spoljašnjosti intenziteta jednakog površini te strane. Dokazati da je rezultanta ovih vektora jednaka nuli. |
[ uranium @ 03.12.2005. 21:17 ] @
Za tetraedar tvrđenje zaista važi:
Neka je 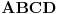 proizvoljan tetraedar, onda je:
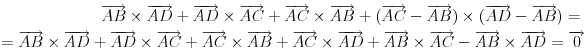 .
Tvrđenje će važiti i za svaki poliedar koji se može dobiti uzastopnim "lepljenjem" tetraedara po nekim njihovim podudarnim stranama, jer su vektori pridruženi tim stranama istog intenziteta, kolinearni, ali suprotnog smera.
E sad, izgleda da se ne može svaki poliedar razbiti na tetraedre:
In 1900, Dehn proved that not every prism can be dissected into a tetrahedron (Lenhard 1962, Ball and Coxeter 1987).
Dakle, moguće je da je postavka pomalo neprecizna... ili je ovaj metod ograničenog dometa (što je i verovatnije  )...
Anyway, it's the end of the road for me  [Ovu poruku je menjao uranium dana 03.12.2005. u 22:21 GMT+1]
[Ovu poruku je menjao uranium dana 03.12.2005. u 22:21 GMT+1][ uranium @ 03.12.2005. 21:34 ] @
U stvari,malo sam požurio 
Mislim da ovaj metod lepljenja ima malih problema. 
Davno sam čitao u nekoj Klarkovoj knjizi, navodno istinit slučaj sa nekog testa inteligencije gde se postavlja pitanje: koliko će imati strana telo koje nastaje lepljenjem po podudarnoj strani, pravilnog tetraedra i pravilne četvorostrane piramide... 
Dakle, obrazloženje koje sam dao u slučaju lepljenja, nije kompletno... ali je metod ipak korektan  [Ovu poruku je menjao uranium dana 03.12.2005. u 22:39 GMT+1]
[Ovu poruku je menjao uranium dana 03.12.2005. u 22:39 GMT+1][ Bojan Basic @ 03.12.2005. 21:47 ] @
Citat: uranium:
Dakle, moguće je da je postavka pomalo neprecizna... ili je ovaj metod ograničenog dometa (što je i verovatnije :) )...
Postavka je korektna, a zaista mi se čini da je metod ograničenog dometa. U svakom slučaju, i jedan deo je više od ničega.
Citat: uranium:
Dakle, obrazloženje koje sam dao u slučaju lepljenja, nije kompletno... ali je metod ipak korektan :)
Nisam siguran šta ovim hoćeš da kažeš. Svakako da tvoj dokaz korektno rešava problem ukoliko razmatramo samo one poliedre koji se mogu dobiti lepljenjem tetraedara. [ uranium @ 03.12.2005. 21:53 ] @
Ako označimo sa 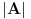 i 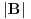 brojeve strana poliedara  i  , onda poliedar dobijen njihovim lepljenjem po podudarnoj strani ne mora imati 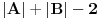 strana  [ Bojan Basic @ 03.12.2005. 22:16 ] @
Slažem se, ali ne vidim kakve to ima veze.
Ukoliko bi se svaki poliedar mogao razložiti na tetraedre onda bi tvoj dokaz bio kompletan. Međutim, to nije tačno i ispostavlja se da si rešio samo specijalan slučaj. Gde se tu pominje broj strana?
[ uranium @ 03.12.2005. 22:56 ] @
E, onda se valjda razumemo 
Ja sam samo napisao da nisam obrazložio sve detalje u slučaju da se posle lepljenja desi da neke 2 strane polaznih poliedara postanu jedna strana (npr. spoje se po jednoj ivici, a leže u istoj ravni). U slučaju kada se to ne desi ja sam imao na umu da se dešava sledeće:
Neka su postojećem poliedru pridruženi vektori 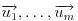 a tetraedru koga dodajemo, vektori  . Neka se lepljenje događa na stranama kojima su pridruženi vektori 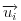 i 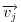 . Vektori su označeni tako da bude: 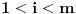 i 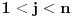 . Dakle, važi: 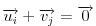 . Pa, će dobijeni poliedar imati pridružene vektore: 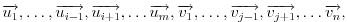 .
Pa iz 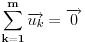 i 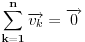 sledi tvrđenje, i tu zaista mislim da je sve korektno.
A ako se desi onaj slučaj, trebalo je da pojasnim da će 2 pridružena vektora u zbiru dati baš vektor pridružen novonastaloj strani (kolinearni su, a površina je aditivna...)
Onima koji su odmah imali u vidu i ovaj poslednji slučaj, se izvinjavam ako sam nepotrebno davio sa detaljima (ja sam naprosto to prevideo u prvi mah).
[ Bojan Basic @ 03.12.2005. 23:05 ] @
Citat: uranium:
A ako se desi onaj slučaj, trebalo je da pojasnim da će 2 pridružena vektora u zbiru dati baš vektor pridružen novonastaloj strani (kolinearni su, a površina je aditivna...)
Aha, sad shvatam. Nisam odmah razumeo da želiš to da naglasiš jer mi se činilo da je to jasno, ali sad su dileme u svakom slučaju razjašnjene.
Citat: uranium:
Onima koji su odmah imali u vidu i ovaj poslednji slučaj, se izvinjavam ako sam nepotrebno davio sa detaljima (ja sam naprosto to prevideo u prvi mah).
Ma nema potrebe da se izvinjavaš, bolje je napisati koji detalj više nego manje, ja jednostavno nisam odmah razumeo da želiš da na to skreneš pažnju i to je sve. [ Farenhajt @ 19.12.2005. 11:38 ] @
Hmmm... Ja ću malo da "kreiram", a onda neka neko to sroči strogo i/ili sažeto.
Ako zamisliš da je poliedar sačinjen samo od letvica, sa šupljim stranama, i ako ga postaviš na neku ravan, pa ga pod bilo kakvim uglom osvetliš paralelnim snopom svetlosti, koji uvek možeš opisati nekim jediničnim vektorom 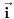 , usmerenim od izvora ka poliedru - uz uslov da taj snop ne sme biti paralelan s projekcionom ravni - onda ćeš kao projekciju na toj ravni dobiti neki poligon, sačinjen od projekcija pojedinih strana poliedra. Pošto je ugao 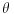 između vektora 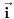 i vektora površine određene strane poliedra 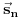 jednak uglu između te strane poliedra i projekcione ravni, površina projekcije strane dobiće se kao 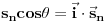 . Odatle sledi da ćemo, ako sumiramo te skalarne proizvode po "osvetljenim" stranama poliedra (dakle, po onima čiji vektori površine zaklapaju najmanje prav ugao s vektorom 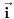 ), a zatim skalarne proizvode po "osenčenim" stranama poliedra (dakle, po onima čiji vektori površine zaklapaju najviše prav ugao s vektorom 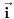 ), dobiti dva iznosa različitog znaka (zbog znaka funkcije 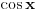 ) ali iste apsolutne vrednosti, koja je jednaka površini projekcije poliedra na ravan. Stoga je 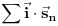 po CELOM poliedru jednaka nuli, a kako je 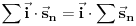 , sledi da je 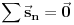 .
[Ovu poruku je menjao Farenhajt dana 20.12.2005. u 18:09 GMT+1][ Bojan Basic @ 19.12.2005. 14:07 ] @
Svaka čast!
To nije ono što sam ja imao u vidu, ali i ovo rešenje mi se zaista sviđa.
Evo totalno drugačijeg, fizičkog pristupa.
Zamislimo da je poliedar iznutra šupalj (kao, recimo, fudbalska lopta) i upumpajmo vazduh u njega. U stanju ravnoteže vektori koji su opisani su upravo sile pritiska vazduha na strane, i njihova rezultanta je očigledno nula jer se radi o stanju ravnoteže.
[ Farenhajt @ 19.12.2005. 15:33 ] @
Odlično!
A elektroinženjeri bi rekli "fluks vektora jačine svakog homogenog polja kroz bilo kakvu zatvorenu površ jednak je nuli" (na šta se praktično svodi moj dokaz) i prešli na sledeći zadatak :)
[Ovu poruku je menjao Farenhajt dana 19.12.2005. u 16:34 GMT+1]
[ zzzz @ 19.12.2005. 23:58 ] @
Citat: Bojan Basic:
Evo totalno drugačijeg, fizičkog pristupa.
Zamislimo da je poliedar iznutra šupalj (kao, recimo, fudbalska lopta) i upumpajmo vazduh u njega. U stanju ravnoteže vektori koji su opisani su upravo sile pritiska vazduha na strane, i njihova rezultanta je očigledno nula jer se radi o stanju ravnoteže.
Dokaz (u hidrostatici) da je pritisak u tekućini skalar,a ne vektor je gotovo onakav
kako je uradio Farenhajt
A ovo \cdot;\dot;\cdots....Klikni na formulu pa vidi kako je napisano!
 [Ovu poruku je menjao zzzz dana 1.1.2006. u 01:05 GMT+1]
[Ovu poruku je menjao zzzz dana 20.12.2005. u 01:07 GMT+1]
[Ovu poruku je menjao zzzz dana 1.1.2006. u 01:05 GMT+1]
[Ovu poruku je menjao zzzz dana 20.12.2005. u 01:07 GMT+1][ Farenhajt @ 20.12.2005. 01:25 ] @
Hvala na pomoći, zzzz! :))
Editovao sam svoju poruku.
A moram da ispravim i grešku koju niko nije zapazio - ali koja neće uticati na tačnost dokaza: Naime, ugao između vektora površine i jediničnog vektora biće jednak uglu između strane poliedra i projekcione ravni samo ako je vektor 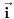 normalan normalan na projekcionu ravan. Uz, dakle, ograničenje da snop svetlosti mora biti normalan na projekcionu ravan, dokaz ostaje isti.
[Ovu poruku je menjao Farenhajt dana 20.12.2005. u 04:57 GMT+1][ Bojan Basic @ 20.12.2005. 12:03 ] @
Citat: zzzz:
Dokaz (u hidrostatici) da je pritisak u tekućini skalar,a ne vektor je gotovo onakav
kako je uradio Farenhajt
Slažem se, ali verujem da velik broj ljudi zna za tu činjenicu ali ne zna dokaz, i stoga smatram da je OK pozvati se na to ne zadirući mnogo u pozadinu svega. [ Farenhajt @ 20.12.2005. 14:10 ] @
I mora se dodati još jedna napomena (koju će neki možda okarakterisati i kao cepidlačenje ili preteranu strogost): Iz činjenice da je 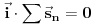 ne može ne može se pravolinijski zaključiti da je 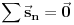 , već samo da je ta suma normalna na 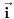 . Međutim, kako se 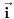 bira proizvoljno, sledi da je 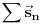 normalna na svaki proizvoljno odabran vektor. E, sada možemo tvrditi da je 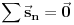 .
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|