[ Lobacev @ 05.12.2005. 11:02 ] @
| Da li dve tačke određuju na jedinstven način i krivu (a ne samo pravu!)? Npr krivu oblika y=a*x*x+b. Ako su zadate dve tačke, da li postoji samo jedna kriva navedenog oblika koja prolazi kroz njih? |
|
[ Lobacev @ 05.12.2005. 11:02 ] @
[ uranium @ 05.12.2005. 13:07 ] @
Ako posmatramo samo polinomijalne krive, onda je odgovor sledeći:
 tačka jedinstveno određuje polinom tačka jedinstveno određuje polinom  -tog stepena. -tog stepena.http://mathworld.wolfram.com/LagrangeInterpolatingPolynomial.html [ tdjokic @ 05.12.2005. 14:28 ] @
Nisam bas neki jak matematicar pa govorim vise laicki: ako imas dve tacke i jednacinu oblika, onda to nisu samo dve tacke, dakle dve tacke, SAME, ne definisu krivu ako nije dat jos neki dodatni podatak / uslov.
[ malada @ 06.12.2005. 20:14 ] @
Dvije tacke neodredjuju krivu tog oblika (koji si napisao), za krivu (i povrsi) nekog oblika imas odredjen broj tacaka koje ih odredjuju.
[ Lobacev @ 07.12.2005. 06:43 ] @
Malada,
koliko tačaka je potrebno da bi se u jednačini y=a*x*x+b odredili koeficijenti a i b ? [Ovu poruku je menjao Lobacev dana 07.12.2005. u 07:45 GMT+1] [ uranium @ 07.12.2005. 12:10 ] @
Znači, pošto je
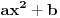 polinom drugog stepena, dovoljne su nam bilo koje tri tačke da bi odredili koeficijente polinom drugog stepena, dovoljne su nam bilo koje tri tačke da bi odredili koeficijente  i i  . .Ali, da ne bude zabune, pošto u tvom primeru ti već znaš jedan koeficijent (koef. uz  je jednak 0) ako bismo pametno birali tačke je jednak 0) ako bismo pametno birali tačke 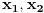 (u ovom slučaju to znači da bude (u ovom slučaju to znači da bude 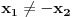 ) onda su nam zapravo potrebne samo dve tačke. ) onda su nam zapravo potrebne samo dve tačke.[Ovu poruku je menjao uranium dana 07.12.2005. u 13:41 GMT+1] [ Lobacev @ 07.12.2005. 12:41 ] @
Da li onda možemo da kažemo sledeće: "DVE RAZLIČITE tačke na jedinstven način određuju krivu oblika y=a*x*x+b" ?
[ uranium @ 07.12.2005. 12:46 ] @
[ Lobacev @ 08.12.2005. 06:54 ] @
Da, iz grafika se lepo vidi da dve tačke NE određuju na jedinstven način krivu datog oblika. Štaviše, dve tačke ne određuju na jedinstven način bilo kakvu krivu ne samo u ravni nego i u prostoru. Ali kako je onda Lobačevski kroz tačku van date prave provukao bezbroj prava paralelnih datoj pravi?
[ uranium @ 08.12.2005. 21:26 ] @
Imam utisak, da je do sad već nekoliko puta došlo do nesporazuma
Taman pomislim kako si hteo da kažeš jedno, a onda me navedeš da pomislim da si hteo ono drugo i tako ad infinitum Ako pričamo o krivama koje su određene jednačinama oblika 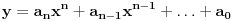 , onda možemo polako da rezimiramo. , onda možemo polako da rezimiramo.Ako si želeo ovakvo tvrđenje: "Svakih  različitih tačaka jedinstveno određuje krivu zadatog oblika." različitih tačaka jedinstveno određuje krivu zadatog oblika." onda bi ono izgledalo ovako: Svakih  različitih tačaka jedinstveno određuje krivu oblika različitih tačaka jedinstveno određuje krivu oblika 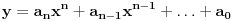 A ako si hteo ovakvo tvrđenje: "Postoji  tačaka tako da one jedinstveno određuju krivu zadanog oblika." tačaka tako da one jedinstveno određuju krivu zadanog oblika."e onda bi to izgledalo ovako: Postoji 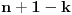 tačaka koje jedinstveno određuju krivu oblika tačaka koje jedinstveno određuju krivu oblika 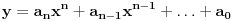 , pri čemu je , pri čemu je  broj koeficijenata koji su jednaki nuli. broj koeficijenata koji su jednaki nuli.Znači, da sam uzeo neke dve različite tačke koje nisu jednako udaljene od  ose, onda bi one jedinstveno odredile krivu oblika ose, onda bi one jedinstveno odredile krivu oblika 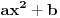 . .A što se Lobačevskog tiče, to je sasvim druga priča [Ovu poruku je menjao uranium dana 08.12.2005. u 22:27 GMT+1] [ Lobacev @ 09.12.2005. 07:46 ] @
A da li ta druga priča (o Lobačevskom i bezbroj paralelnih prava) ima kraj?
[Ovu poruku je menjao Lobacev dana 09.12.2005. u 08:46 GMT+1] [ malada @ 22.01.2006. 22:35 ] @
Ima zove se hiperbolicka geometrija
[ Lobacev @ 23.01.2006. 13:40 ] @
Drugi kraj je u eliptičkoj geometriji. A da li ima još koji ogranak?
[ Lobacev @ 16.02.2006. 10:51 ] @
Da malo poguram diskusiju:
- koren iz negativnog broja, npr. iz -25 je i*5, gde je i*i=-1. Tu nema sekiracije iako u prirodi nema brojeva kao što je broj i: Kada se broje ovce ili računa površina njive - nigde se ne spominje i. - ali zato se živi izsekirasmo zbog hiperbolične i eliptične geometrije - kako to da se kroz tačku van prave ne može povući nijedna paralelna prava ili se može provući njih bezbroj mnogo? [ peddja_stankovic @ 16.02.2006. 12:44 ] @
@Lobacev
Mnogi me studeni pitaju cemu sve to. I danas se kod nekih plemena broji 1,2,3,4,5,puno. U medjuvremenu je ljudska misao evoluirala pa se rodila ideja o prirodnim brojevima vecim od 5. Nula je kao broj relativno novijeg datuma. Sto se tice negativnih brojeva, na primer -200 znaci da smo 200 evra duzni nekome, koliko smo udaljeni od "pozitivne nule". Tesko bi resili realne probleme bez negativnih brojeva. Resenje jednacine x^2 = -4 nije realan broj nego 2i. Pa to bi moglo da se shvati da smo 2 jedinice daleko od realnog resenja. Bez kompleksnih brojeva ne bismo mogli da resavamo realne diferencijalne jednacine (pa bismo bili uskraceni za fundamentalan odgovor na pitanje da li ce mrav da stigne na kraj trake koja se rastezze - vidi jednu od prethodnih tema). [Ovu poruku je menjao peddja_stankovic dana 16.02.2006. u 13:46 GMT+1] [ srki @ 16.02.2006. 13:06 ] @
[ Lobacev @ 16.02.2006. 13:10 ] @
Srki, svaka čast na preciznosti. Takođe svaka čast i na rešenju onog zadatka sa Čamcem i sidrom. Ali sada treba da diskutujemo o smislu i značenju eliptične i hiperbilične geometrije, zar ne?
[ Farenhajt @ 16.02.2006. 13:59 ] @
Zašto bi matematika morala da se bavi samo makroskopskim, vidljivim i onim što je prijemčivo samo predškolskom umu (njivama, ovčicama, brojanjem na prste)? Primeni malo njutnovske mehanike na atomskom nivou, ili euklidske geometrije u astrofizici, pa nam javi šta si otkrio.
Kako mi na džigericu idu likovi koji bi matematiku sveli na piljarsko sabiranje (doduše, sad više ni to ne moraju, pošto čitači bar-kodova rade kasirski posao...) [ Lobacev @ 16.02.2006. 14:21 ] @
Pa matematika je tako i počela da se razvija - zbog praktičnih potreba iz svakidašnjeg života. Sada već možemo da obučemo beli mantil, zavalimo se u fotelju, grickamo kraj od olovke i gledajući u plafon sa visine pljuckamo na sve koji pokušavaju da složene stvari objasne na najjednostavniji mogući način.
[ Farenhajt @ 16.02.2006. 16:27 ] @
Niko ne pljucka na one koji traže najjednostavnije moguće objašnjenje. Eventualno se pljucka samo na one koji najjednostavnije moguće objašnjenje odbacuju jer je ono za njihovu moć poimanja preterano komplikovano ("što se ne da na prste izbrojati, ne postoji").
[Ovu poruku je menjao Farenhajt dana 16.02.2006. u 17:30 GMT+1] [ srki @ 16.02.2006. 20:24 ] @
The shortest path between two truths in the real domain
passes through the complex domain. Jacques Hadamard [ Lobacev @ 24.02.2006. 10:19 ] @
Da opet malo poguram temu. Kako bi odgovorili na sledeća pitanja:
a) Da li je "debljina" prave: I) nula mm (ili Km, svejedno); II) beskonačno mala, t.j. --> 0; III) o takvoj temi se u poštenim matematičarskim porodicama ne razgovara; b) Da li je "debljina" ili "prečnik" tačke: I) nula mm (ili Km, svejedno); II) beskonačno mala, t.j. --> 0; III) o takvoj temi se u poštenim matematičarskim porodicama ne razgovara; [ chupcko @ 24.02.2006. 13:50 ] @
Da li si nekada citao neku knjigu "Elementi" ?
http://www.matf.bg.ac.yu/nastavno/zlucic/ A i malo je glupo da nekim pojmovima koji mozda i ne postoje da dajes fizicke osobine. Mislim gde stati, koja je temperatura tacke, a koja visina :). Da li je tacka u stereometriji je pljosnjata ili je loptasta :). Da li tacka mora biti bas krug :). Na srecu postoji nesto sto ja zovem "inzinjerska matematika" i ono sto ja zovem "filozofska matematika", i mislim da lepo mogu da postoje obe dok smo svesni da ima razlike :). Eto cisto me i zanima da li je tacka manja od atoma :)))). [ Lobacev @ 24.02.2006. 14:23 ] @
Pitanje je postavljeno u polušaljivom tonu, a ako si primetio, nudi se i odgovor da "debljina" može da teži i nuli ->0. Ponekad nije zgoreg ni stare istine podvrći kritici. Nisam mislio da se baš uzme mikrometarski zavrtanj pa da se izmere dimenzije. Mislim da čitava gužva oko pomenute tri geometrije potiče iz odnosa beskonačno malih veličina. Iako su i tačka i prava "bez debljine", ipak se ove njihove "dimenzije" implicitno stavljaju u relativan odnos kada se kaže "prava prolazi kroz tačku". Zna se da količnik dve beskonačno male veličine može biti i nula, i beskonačno i neki konačan broj.
[ chupcko @ 25.02.2006. 21:30 ] @
Pa uf, i ja se salim, zar ne :)
Gde si cuo da prava prolazi kroz tacku ? Ako ces bas formalno uvek se kaze da prava sadrzi (moze se i u skupovnu smislu reci) tacku :). Ima jedna lepa knjiga, "osnovi geometrije" od zorana lucica, prouci barem prvoh 100 strana pa nastavi sam semnatickim tumacenjem necega sto je strogo formalno definisano :). I licni savet, nemoj da se dalje upetljavas, mozda naidjes na nekog ko nije polagao geometriju pre 10 godina, nego na nekog ko to zna mnogoooooo bolje :). [ Lobacev @ 27.02.2006. 06:44 ] @
Chupcko, otkuda sad ta malodušnost? Da li to znači da treba svim rekareativcima reći da se ne bave trčanjem jer nikada neće oboriti olimpijski rekord?
[Ovu poruku je menjao Lobacev dana 27.02.2006. u 07:53 GMT+1] [ chupcko @ 27.02.2006. 08:47 ] @
Samo se ti bavi, ali na pravi nacin :). To jest kada izvalis glupost ocekuj sarkazam.
Ajde onda da izlozimo dokaz da je krokodil duzi nego sto je siri. Lema 1: Krokodil je duzi nego sto je zeleniji. Dokaz: Krokodil je dugacak sa gornje i donje strane a zelen je samo sa gornja strane, dakle krokodil je duzi nego sto je zeleniji. QED Lema 2: Krokodil je zeleniji nego sto je siri. Dokaz: Krokodil je zelen i po duzini i po sirini, a sirok je samo po siirini, dakle krokodil je zeleniji nego sto je siri. QED Dokaz se lako izvodi iz leme 1 i leme 2. [ Lobacev @ 27.02.2006. 08:58 ] @
Početne premise ti nisu dobre. Krokodil je odozgo SIVO-ZELEN a odozdo više BEŽ boje. Modifikuj dokaz.
[ Bojan Basic @ 27.02.2006. 10:02 ] @
Ode tema u offtopic.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|