[ kajla @ 11.10.2002. 15:59 ] @
1. Neka je P(x) polinom n-tog stepena koji je simetričan. Neka je Q(x) polinom takav da je P(x) = (x+1)Q(x). Dokazati da je polinom Q(x) takođe simetričan.

2. Neka je P(x) polinom n-tog stepena koji je kososimetričan. Neka je Q(x) polinom takav da je P(x) = (x-1)Q(x). Dokazati da je polinom Q(x) takođe simetričan.

Polinom je simetričan ako su koeficijenti uz xk i xn-k jednaki.

Polinom je kososimetričan ako su koeficijenti uz xk i xn-k suprotni brojevi.

poz.
[ filmil @ 17.10.2002. 12:14 ] @
Evo, više da probam ovaj ...

Ako je

, gde je

Takođe je

Ako je

, koeficijenti polinoma
su dati sa



Potrebno je da se vidi da je da bi polinom bio simetričan jer je .



Imamo prema uslovu zadatka:



i



Pa je:



A to je ono što nam treba.

Uh, oznojih se od ovog -a.
f
[ shiggy @ 22.10.2002. 16:21 ] @
Kad ste vec kod polinoma, da nema neko klasu polinoma u cpp koju bi mogao da koristim u domacim i seminarskim radovima?


Unapred hvala
[ kajla @ 22.10.2002. 18:08 ] @
Trebalo je dokazati da je polinom koji se dobija deljenjem simetričnog polinoma sa x+1 je takođe simetričan, filmil ti si dokazao da je polinom koji se dobija množenjem simetričnog polinoma sa x+1 takođe simetričan.

poz.
[ filmil @ 22.10.2002. 23:48 ] @
Dragi moji prijatelji, tako vam je to kad je jezik dugacak a
pamet kratka. :(

No dobro, probacu da se ispravim, mada bi lepo bilo da matematicki deo
populacije dostavi i elegantno resenje. Zadrzacu notaciju iz
prethodnog resenja.

Elem, prosli put sam sa pokazao da vazi:



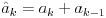
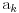
Ako zapisemo ovo drugacije, mozemo izraziti preko
:



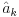
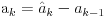
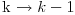
Uz pomoc ove jednacine, stavljanjem mozemo
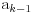
eliminisati zavisnost od uvodeci u isto vreme
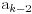
zavisnost od . Raspakivanjem ovog izraza, zatim
metodom gledanja pa primenom indukcije moze se doci do:



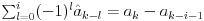
Granica sumiranja se moze pronaci iz uslova da je
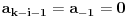
, tj.



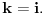
Dakle:



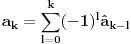
jeste izraz koji pokazuje kako koeficijenti kolicnika zavise od
koeficijenata polinoma deljenika.

Ako se ovo preuredi tako da nam uz koeficijente polinoma ispod sume
ostane samo nemi indeks, smenom se dobija:



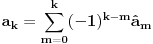
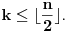
Pretpostavimo sada da je (ne gubi se na opstosti resenja jer inace samo
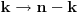
smenimo i idemo dalje).

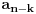
Za clan imamo da je:



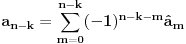
Poslednji izraz se moze prepisati imajuci u vidu polaznu tvrdnju o
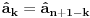
simetriji koeficijenata polinoma: tako sto ovu transformaciju primenimo na svaki clan
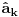
pa dobijamo:



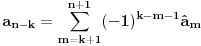
Medjutim, ako se prisetimo da je polazni polinom bio:



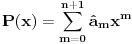
Vidimo da je:



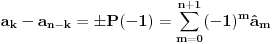
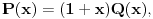
Ali, gle cuda, posto je imamo da je
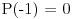
pa je:



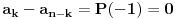
ili konacno



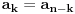
Nadam se da je sada u redu.

f