[ petarm @ 08.12.2005. 14:04 ] @
| Trebalo bi mi sto vise ideja za dokaz da je skup realnih brojeva neprebrojiv. Odnosno da se ne moze uspostaviti bijekcija izmedju njega i skupa prirodnih brojeva? Posaljite svoje ideje ili gotove dokaze! |
|
[ petarm @ 08.12.2005. 14:04 ] @
[ maximus_1 @ 09.12.2005. 14:01 ] @
Mene zanima koji su skupovi prebrojivo beskonačni, a koji neprebrojivo beskonačni?
[ peddja_stankovic @ 10.12.2005. 06:09 ] @
Dokazimo da je (0,1) neprebrojiv.
Pretpostavimo suprotno da (0,1) i N imaju istu moc, tj. da se svi realni brojevi iz (0,1) mogu urediti u niz: 0.d11d12d13...d1n... 0.d21d22d23...d1n... ................ 0.dn1dn2dn3...dnn... ................ gde su brojevi dij iz skupa {0,1,...,9}, i,j iz N. Uzmimo sad realan broj a takav da je a=0.d1d2d3....dn.... gde je d1 razlicito od d11, d2 razlicito od d22, ........ dn razlicito od dnn, ........ i dk iz skupa brojeva {0,1,...,9}. Ocigledno je da je a iz intervala (0,1) i da se a razlikuje od svih brojeva u nizu bar u jednoj cifri. To je kontradikcija. Dakle svi realni brojevi iz intervala (0,1) se ne mogu urediti u beskonacan niz sto znaci da je (0,1) neprebrojiv. [Ovu poruku je menjao peddja_stankovic dana 10.12.2005. u 07:10 GMT+1] [ uranium @ 11.12.2005. 15:54 ] @
Evo jednog dokaza koji sam svojevremeno video u Natanson-u.
Dokazaćemo da je segment 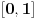 neprebrojiv. neprebrojiv.Neka je 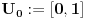 . .Pretpostavimo suprotno, tj. da je 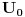 prebrojiv. prebrojiv.Onda sledi da sve tačke skupa 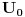 možemo poređati u niz: možemo poređati u niz:  Sada podelimo 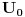 na tri jednaka dela: na tri jednaka dela:  , ,  , , 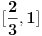 . Očigledno je da barem jedan od ovih segmenata ne sadrži tačku . Očigledno je da barem jedan od ovih segmenata ne sadrži tačku 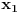 , označimo "najlevljeg" od takvih sa , označimo "najlevljeg" od takvih sa 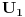 . .Podelimo 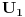 na 3 jednaka segmenta, i opet barem jedan od njih ne sadrži tačku na 3 jednaka segmenta, i opet barem jedan od njih ne sadrži tačku 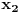 , pa označimo sa , pa označimo sa 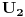 "najlevljeg" od takvih. "najlevljeg" od takvih.Ako nastavimo opisani postupak, dobićemo niz umetnutih odsečaka:  sa osobinom da za svako sa osobinom da za svako 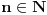  . Primetimo da je dužina segmenta . Primetimo da je dužina segmenta 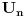 jednaka jednaka 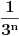 . Dakle, imamo niz umetnutih odsečaka čija dužina teži nuli, pa na osnovu poznate Kantorove teoreme sledi da postoji jedinstvena tačka . Dakle, imamo niz umetnutih odsečaka čija dužina teži nuli, pa na osnovu poznate Kantorove teoreme sledi da postoji jedinstvena tačka 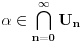 . .Pošto je 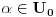 , onda tačka , onda tačka  mora biti u nizu mora biti u nizu 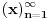 . Dakle, postoji . Dakle, postoji 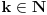 tako da tako da 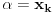 . .Međutim, to je kontradikcija, jer 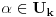 a a 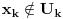 , pa ne može biti , pa ne može biti 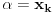 . .Glavni razlog, zbog koga sam ovo napisao, je to što mi se zaista čini da dokaz koji je dao peddja_stankovic (a koji se može naći na primer kod Kadelburga) ima ozbiljnih mana. Zamerka je u tome što je konstrukcija kojom se generiše broj  ostvariva akko broj ostvariva akko broj  nije na spisku, a to je baš ono što se i htelo dokazati... nije na spisku, a to je baš ono što se i htelo dokazati...Znam iz razgovora sa S. B. Prešićem da i on (iz nekih sličnih razloga) misli da je pomenuti dokaz pogrešan. Voleo bih da čujem još nečije mišljenje o ovome, jer mislim da je pitanje veoma suptilno i duboko. [ Bojan Basic @ 11.12.2005. 16:52 ] @
Čuo sam neke priče o tome da je Kantorom dijagonalni dokaz pogrešan, međutim nisam nikad to detaljnije istraživao. Ipak, drago mi je što je potegnuto ovo pitanje da možemo da vidimo u kom grmu leži zec.
Citat: Mene bi zanimalo dodatno pojašnjenje ove rečenice. Naime, pretpostavimo da lista postoji. Svakako je možemo zapisati onako kako je peddja_stankovic uradio. Onda idemo redom po dijagonali i jednostavno zamenimo svaku cifru. Moram priznati da ne vidim gde prilikom te konstrukcije pretpostavljamo da broj  nije na spisku, meni se čini da su naše jedine pretpostavke u ovom koraku: nije na spisku, meni se čini da su naše jedine pretpostavke u ovom koraku:1) da od svake cifre postoji različita; 2) da svaki (beskonačan) niz cifara određuje jedinstven realan broj iz posmatranog intervala. [ uranium @ 12.12.2005. 08:00 ] @
Citat: Mislio sam da je to jasno pa nisam eksplicitno naglasio: Ako bismo znali u napred da je broj  na spisku, on bi se razlikovao od samog sebe u barem jednoj cifri! I (re)konstrukcija ne bi prošla! na spisku, on bi se razlikovao od samog sebe u barem jednoj cifri! I (re)konstrukcija ne bi prošla!Ajde da pokušamo još nešto. Primetimo da je prvo napravljen skup  , pa onda spisak, pa je tek onda (nekorektno) definisan broj , pa onda spisak, pa je tek onda (nekorektno) definisan broj  . .Imamo prihvaćenu pretpostavku da smo sve brojeve iz intervala  ubacili na spisak, i nad tom činjenicom ne smemo da "zažmurimo". ubacili na spisak, i nad tom činjenicom ne smemo da "zažmurimo".Zapitajmo se da li postoji broj u  , koji bi se od , koji bi se od  -tog broja sa spiska razlikovao u -tog broja sa spiska razlikovao u  -toj cifri. Ako takav broj postoji, on ne može biti na spisku (po definiciji) a morao bi biti (zbog sveobuhvatnosti spiska)- dakle, ne postoji! -toj cifri. Ako takav broj postoji, on ne može biti na spisku (po definiciji) a morao bi biti (zbog sveobuhvatnosti spiska)- dakle, ne postoji!U stvari u prethodnom bi zaključak trebalo da bude: ne postoji broj ili ne postoji spisak. Ali kako god, broj neće postojati. Da obrazložim sada onu ekvivalenciju koja je citirana: Prvi smer: Ako je konstrukcija moguća, onda broj  nije na spisku. To sledi iz definicije broja nije na spisku. To sledi iz definicije broja  . .Drugi smer: Neka je  proizvoljan prebrojiv skup brojeva iz intervala proizvoljan prebrojiv skup brojeva iz intervala  . Ako je . Ako je 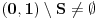 , onda je zaista moguće napraviti broj sa traženim svojstvima, jer on ne bi ni bio u pomenutom skupu , onda je zaista moguće napraviti broj sa traženim svojstvima, jer on ne bi ni bio u pomenutom skupu  . . Naravno, ne mislim da je ovime sve rečeno ili "rasčišćeno" [ Nedeljko @ 12.12.2005. 08:03 ] @
Peđa Stanković je dokazao da ne postoji spisak svih realnih brojeva iz intervala [0,1], što je i trebalo dokazati. On je pretpostavio suprotno, da spisak (koji sadrži sve elemente intervala [0,1]) postoji, pa je konstruisao jedan element za koji je dokazao da pripada odsečku, a da nije u spisku. Dobijena kontradikcija pokazuje da polazna pretpostavka nije tačna, što je i trebalo dokazati.
Jedina mana pomenutog dokaza je što proizvoljan niz cifara ne određuje realan broj na injektivan način. Recimo, 0,00999... = 0,01000. Međutim, na pomenuti način možemo konstruisati broj čija je svaka cifra na prime 5 ili 6. Onda je sve u redu. No, taj dokaz pretpostavlja poznavanje odgovarajuće teorije vezane za beskonačan decimalni razvoj realnih brojeva itd. Profesor S. B. Prešić je razmatrao ovakvu dijagonalizaciju u nekim drugim kontekstima vezanim za algoritamsku izračunljivost i konstruktibilnost. Do je druga stvar. [ Bojan Basic @ 13.12.2005. 11:54 ] @
Citat: Naravno. Tako ulećemo u kontradikciju i sledi da je naša pretpostavka da spisak postoji pogrešna. I dalje ne shvatam? Citat: Prvo smo definisali neki beskonačan niz cifara (slažeš se da to možemo da uradimo bez ikakvih pretpostavki), i onda smo rekli: "Neka je broj  dobijen tako što ovaj niz cifara poređamo iza decimalnog zareza". Da li se slažeš da svaki beskonačan niz cifara određuje neki realan broj? Ukoliko odgovoriš potvrdno onda zaista ne shvatam gde je nesuglasica. dobijen tako što ovaj niz cifara poređamo iza decimalnog zareza". Da li se slažeš da svaki beskonačan niz cifara određuje neki realan broj? Ukoliko odgovoriš potvrdno onda zaista ne shvatam gde je nesuglasica.Citat: uranium: U stvari u prethodnom bi zaključak trebalo da bude: ne postoji broj ili ne postoji spisak. Slažem se. No, u prethodnom pasusu sam objasnio zašto broj mora da postoji (naravno, možeš da se ne složiš, ukaži gde misliš da grešim pa ćemo nastaviti), i tako nam ostaje jedina varijanta da spisak ne postoji, a to je ono što želimo da pokažemo. [ uranium @ 13.12.2005. 13:39 ] @
Kao prvo nadam se da se svi slažemo oko toga da je ceo skup
 unapred dat. Dakle, nemamo mi tu šta dodatno da konstruišemo neke brojeve, svi postojeći brojevi su već dati. Mi eventualno možemo da pokušamo da opišemo neki od postojećih. unapred dat. Dakle, nemamo mi tu šta dodatno da konstruišemo neke brojeve, svi postojeći brojevi su već dati. Mi eventualno možemo da pokušamo da opišemo neki od postojećih.Pa evo: ako je dat neki prebrojiv skup 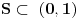 , opišimo broj preko njegovog decimalnog razvoja na standardan način: , opišimo broj preko njegovog decimalnog razvoja na standardan način: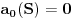 i i 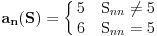 Pogledajmo sada da li je ova definicija korektna. Ako ovaj broj zaista postoji, on je postojao istog onog "momenta" kada je definisan i skup  . .Dalje, ako postoji, onda je ili 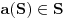 ili je ili je 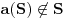 . .Jasno je da prva mogućnost otpada. Znači ostaje zaključak: ako 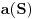 postoji, onda postoji, onda 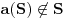 . .Možemo sada sve to reći i ovako: pomenuti postupak nije ništa drugo, nego način da se opiše jedan broj koji nije u datom prebrojivom skupu. Spor nastaje onda kada uzmemo da je 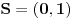 . .Tvrdim da definicija broja 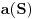 u tom slučaju nije korektna, jer bilo da verujemo (u odgovarajućem koraku dokaza) da je skup u tom slučaju nije korektna, jer bilo da verujemo (u odgovarajućem koraku dokaza) da je skup  prebrojiv ili ne, nema šta više da se opiše van skupa prebrojiv ili ne, nema šta više da se opiše van skupa  . .[Ovu poruku je menjao uranium dana 13.12.2005. u 15:25 GMT+1] [ Bojan Basic @ 13.12.2005. 19:54 ] @
Citat: Ali ko je, zaboga, bilo šta tražio van skupa  ? Naprotiv, broj ? Naprotiv, broj  koji smo pronašli mora da pripada skupu koji smo pronašli mora da pripada skupu  jer svaki beskonačan niz cifara određuje jedan broj iz tog skupa, a naš broj jer svaki beskonačan niz cifara određuje jedan broj iz tog skupa, a naš broj  upravo jeste jedan beskonačan niz cifara. E onda kažemo: "Ovaj broj pripada skupu upravo jeste jedan beskonačan niz cifara. E onda kažemo: "Ovaj broj pripada skupu  , ali, gle čuda, on ne može da se nađe na onoj listi. Dakle, pošto smo zamislili da postoji lista koja ređa sve brojeve iz , ali, gle čuda, on ne može da se nađe na onoj listi. Dakle, pošto smo zamislili da postoji lista koja ređa sve brojeve iz  , a ipak smo našli broj iz tog skupa koji nije na toj listi, sledi da takva lista ne postoji". , a ipak smo našli broj iz tog skupa koji nije na toj listi, sledi da takva lista ne postoji".[ uranium @ 13.12.2005. 20:36 ] @
Ja se sve vreme slažem da svaki niz cifara određuje jedan broj iz
 , ali se ne slažem sa svakim postupkom određivanja tog niza. , ali se ne slažem sa svakim postupkom određivanja tog niza.Pa mislio sam da se slažemo oko ovoga: Citat: uranium: pomenuti postupak nije ništa drugo, nego način da se opiše jedan broj koji nije u datom prebrojivom skupu. Učiniću još jedan napor da obrazložim ovaj deo: Neka je 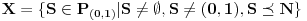 i neka je i neka je 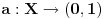 funkcija definisana kao i ranije: funkcija definisana kao i ranije:Citat: Ranije smo već ustanovili da za svako 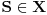 , važi , važi 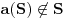 . Pokušaj proširivanja domena f-je . Pokušaj proširivanja domena f-je  tako da u domen upadne i tako da u domen upadne i  ne bi uspeo, jer bi odmah dobili već toliko puta pominjanu kontradikciju. ne bi uspeo, jer bi odmah dobili već toliko puta pominjanu kontradikciju. Dakle, ako već znamo da f-ja  ima osobinu da za svako ima osobinu da za svako  iz svog domena važi iz svog domena važi  , šta nam daje za pravo da za , šta nam daje za pravo da za  uzmemo uzmemo  i pri tom i dalje tvrdimo da smo time generisali neki broj?! i pri tom i dalje tvrdimo da smo time generisali neki broj?![Ovu poruku je menjao uranium dana 13.12.2005. u 22:51 GMT+1] [ Bojan Basic @ 13.12.2005. 22:27 ] @
Ti prilaziš problemu malo sa zaobilazne strane, sad otprilike počinjem da shvatam tvoj pristup. No, nema veze, kako god mu pristupio rezultat je isti. Dozvoli mi da citiram tvoju rečenicu:
Citat: Zar ti se ne čini da, pošto funkcija "radi" za prebrojive  , a mi ne možemo da za , a mi ne možemo da za  uzmemo uzmemo  , sledi da je , sledi da je  neprebrojiv? neprebrojiv?edit: greška u kucanju [Ovu poruku je menjao Bojan Basic dana 14.12.2005. u 00:45 GMT+1] [ uranium @ 13.12.2005. 22:37 ] @
Citat: Naravno, pomislio sam  . Jer ko što rekoh . Jer ko što rekoh Dakle, u najmanju ruku pošteno bi bilo zaključiti da funkcija ne radi zato što je  neprebrojiv ili zato što je taj skup prevelik u smislu inkluzije i definicije f-je neprebrojiv ili zato što je taj skup prevelik u smislu inkluzije i definicije f-je  . .S druge strane, ako bi f-ji "podmetnuo" kao prebrojiv neki neprebrojiv pravi podskup od  ne bi se pojavila nikakva kontradikcija. S tim u vezi, potencijalno imam i jednu zanimljivu konstrukciju, koja bi trebalo da pokaže da kontradikciju nije uzrokovala neprebrojivost skupa ne bi se pojavila nikakva kontradikcija. S tim u vezi, potencijalno imam i jednu zanimljivu konstrukciju, koja bi trebalo da pokaže da kontradikciju nije uzrokovala neprebrojivost skupa  , međutim ne mogu da je prikažem dok ne otklonim sve eventualne propuste. , međutim ne mogu da je prikažem dok ne otklonim sve eventualne propuste.[Ovu poruku je menjao uranium dana 13.12.2005. u 23:44 GMT+1] [ Bojan Basic @ 13.12.2005. 22:47 ] @
I to je kontradikcija, pa sledi da je pretpostavka netačna. Šta je pretpostavka? Pa pretpostavili smo da se  može poređati u niz, i sad dolazimo do toga da to nije tačno. može poređati u niz, i sad dolazimo do toga da to nije tačno.Siguran sam da si i ranije koristio metodu kontradikcije prilikom rešavanja nekih zadataka, zašto misliš da se ovaj put to ne može primeniti? Citat: Ako kažeš prevelik u smislu veći od prebrojivog onda je to ono što i hoćemo da kažemo, u suprotnom ne shvatam šta podrazumevaš pod pojmom prevelik. Citat: Slažem se. No, šta nam to govori? Ništa, govori nam samo toliko da se ova metoda ne može iskoristiti u opštem slučaju za dokaz neprebrojivosti nekih pravih podskupa skupa  već je uspešna samo u ovom slučaju. već je uspešna samo u ovom slučaju.[ uranium @ 13.12.2005. 23:04 ] @
Potpuno se slažem sa poslednjom rečenicom.
Citat: Bojan Basic: Ako kažeš prevelik u smislu veći od prebrojivog onda je to ono što i hoćemo da kažemo, u suprotnom ne shvatam šta podrazumevaš pod pojmom prevelik. naprosto f-ja je napravljena tako da radi za prave podskupove skupa  i ništa više od toga. i ništa više od toga. A to što dobijamo da je  bi moglo biti posledica implicitne pretpostavke da broj bi moglo biti posledica implicitne pretpostavke da broj 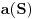 postoji i samo je pokazatelj nekih ograničenja koje je nametnula definicija f-je (i tu ne mislim na ograničenje o prebrojivosti postoji i samo je pokazatelj nekih ograničenja koje je nametnula definicija f-je (i tu ne mislim na ograničenje o prebrojivosti [Ovu poruku je menjao uranium dana 14.12.2005. u 00:06 GMT+1] [ Bojan Basic @ 13.12.2005. 23:14 ] @
[ uranium @ 13.12.2005. 23:28 ] @
[ Bojan Basic @ 13.12.2005. 23:40 ] @
Dobro,
 . Ukoliko je . Ukoliko je 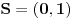 dobijamo dobijamo  , što je nemoguće, u čemu se slažemo (složili su se već i vrapci pored nas dvojice , što je nemoguće, u čemu se slažemo (složili su se već i vrapci pored nas dvojice Imamo implikaciju oblika 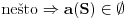 , odnosno , odnosno 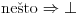 . Iz toga sledi da . Iz toga sledi da  mora biti netačno. A to mora biti netačno. A to  je pretpostavka da postoji lista koja odgovara skupu je pretpostavka da postoji lista koja odgovara skupu  . .To i dalje ne implicira da je  netačno ukoliko uzmemo za netačno ukoliko uzmemo za  neki pravi, neprebrojiv podskup od neki pravi, neprebrojiv podskup od  (zapravo, to jeste tad netačno, ali ne sledi odavde već moramo ići drugim putem). Međutim, sad nam treba samo ovaj slučaj, i za njega imamo to što hoćemo. (zapravo, to jeste tad netačno, ali ne sledi odavde već moramo ići drugim putem). Međutim, sad nam treba samo ovaj slučaj, i za njega imamo to što hoćemo.[ uranium @ 14.12.2005. 00:03 ] @
Sa poslednjim pasusom se (ponovo
Stvar je samo u tome, da ja odbijam da me bilo šta ( a pogotovu  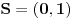 , jer je to potpuno protivno nameni f-je (a to je, da podsetim: "bekstvo" iz zadatog podskupa). Dakle u tom, inkriminisanom slučaju, nemamo kud da pobegnemo i u tome nema ništa kontradiktorno. , jer je to potpuno protivno nameni f-je (a to je, da podsetim: "bekstvo" iz zadatog podskupa). Dakle u tom, inkriminisanom slučaju, nemamo kud da pobegnemo i u tome nema ništa kontradiktorno.@Bojan Bašić: Za slučaj da se ne slažeš sa prethodnim (a što je gotovo izvesno  sadrži i pretpostavku o postojanju broja sadrži i pretpostavku o postojanju broja 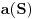 . I onda ako dođeš do onoga što smatraš kontradikcijom, pada i pomenuta pretpostavka o egzistenciji. . I onda ako dođeš do onoga što smatraš kontradikcijom, pada i pomenuta pretpostavka o egzistenciji.I na kraju, da se našalim sa svima koji misle da je dokazano nepostojanje liste: ako ne postoji lista, onda ne postoji ni broj generisan nepostojećom listom! [ Bojan Basic @ 14.12.2005. 00:13 ] @
Citat: uranium: Dakle u tom, inkriminisanom slučaju, nemamo kud da pobegnemo i u tome nema ništa kontradiktorno. Ali ja tvrdim da je upravo to što iako mi nemamo kud, ipak uspevamo da pobegnemo kontradikcija, i ona nam obara pretpostavku, a sve to nam savršeno odgovara. Citat: Slažem se da sadrži i pretpostavku o postoanju broja 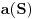 , ali verujem da se i ti slažeš da sadrži i pretpostavku o postojanju liste. E sad, pošto smo lupili glavom u zid, da vidimo šta zapravo pada. Pada bar jedna od te dve pretpostavke (ne neophodno obe! - De Morganov zakon). Može li da padne postojanje broja , ali verujem da se i ti slažeš da sadrži i pretpostavku o postojanju liste. E sad, pošto smo lupili glavom u zid, da vidimo šta zapravo pada. Pada bar jedna od te dve pretpostavke (ne neophodno obe! - De Morganov zakon). Može li da padne postojanje broja 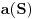 ? E, tu ja kažem da ne može, jer smo njega sasvim legalno dobili (koristili smo pretpostavke koje sam već ranije pominjao: da od svake cifre postoji različita i da svaki beskonačan niz cifara obrazuje realan broj, apsolutno ništa više). Dakle, jedino što nam preostaje je da pada pretpostavka o postojanju same liste. ? E, tu ja kažem da ne može, jer smo njega sasvim legalno dobili (koristili smo pretpostavke koje sam već ranije pominjao: da od svake cifre postoji različita i da svaki beskonačan niz cifara obrazuje realan broj, apsolutno ništa više). Dakle, jedino što nam preostaje je da pada pretpostavka o postojanju same liste.Citat: uranium: I na kraju, da se našalim sa svima koji misle da je dokazano nepostojanje liste: ako ne postoji lista, onda ne postoji ni broj generisan nepostojećom listom! Dobro je da si naglasio da je ovo šala, inače... [ uranium @ 14.12.2005. 00:28 ] @
A zašto ne bi jednostavno odustali od bekstva, kad već imamo garanciju da je neizvodljivo?
Ja ponovo tvrdim da uspešnost bekstva esencijalno zavisi od međusobnog odnosa skupa iz koga bežimo i skupa u koji bežimo, dakle mislim da nije dovoljan formalan algoritam koga treba pratiti da bi nam osigurao bekstvo i ne možemo uzeti skup  samo kao sirove podatke i pustiti "mašinu" da odradi svoje, jer će se na kraju desiti (barem u našem slučaju) da mašina krene da obrađuje samu sebe! Znači moramo na neki način interpretirati podatke, pre nego ih upotrebimo. samo kao sirove podatke i pustiti "mašinu" da odradi svoje, jer će se na kraju desiti (barem u našem slučaju) da mašina krene da obrađuje samu sebe! Znači moramo na neki način interpretirati podatke, pre nego ih upotrebimo.Nadam se da nisam preterao sa analogijama. [ Bojan Basic @ 14.12.2005. 00:37 ] @
Citat: uranium: A zašto ne bi jednostavno odustali od bekstva, kad već imamo garanciju da je neizvodljivo? Ček, sad sam se pogubio. Čini mi se da je ovo otprilike slično pitanju: "A zašto ne odustanemo od rešavanja zadatka?" Možeš ti da odustaneš od bekstva, ali tako nećeš rešiti zadatak (ili možda hoćeš, ali može i ovako). Citat: uranium: Mi upravo pokušajem da uradimo nešto nemoguće, izazivamo kontradikciju. Niko tebi ne brani da probaš da uradiš nešto nemoguće, naravno legalnim metodama. I ti, dakle, sasvim legalno probaš da pobegneš na sasvim legalan način i onda kažeš: "Gle čuda, uspeo sam". To je savršena kontradikcija. Zapravo, voleo bih da mi navedeš bar jedan primer nekog zadatka koji se može rešiti metodom kontradikcije a da u njemu nema uspelog ispunjavanja nečeg nemogućeg (što kontradikcija i jeste, red reči je bitan). [ uranium @ 14.12.2005. 00:49 ] @
Ja samo kažem da je to kad mi stavimo
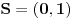 isto kao kad stavimo isto kao kad stavimo 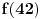 za f-ju za f-ju 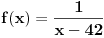 i posle kukamo :"Jao, vidi šta mi se desilo" (opširnije). i posle kukamo :"Jao, vidi šta mi se desilo" (opširnije).Dalje, ako u dokazu prvo pretpostavimo da je skup  prebrojiv, hajde onda da se zagnjurimo u postupak opisivanja traženog broja. Ako je uopšte moguće opisati taj broj, on se već nalazi u skupu prebrojiv, hajde onda da se zagnjurimo u postupak opisivanja traženog broja. Ako je uopšte moguće opisati taj broj, on se već nalazi u skupu  jedino što mi u prvom trenutku ne bi umeli da ga "prepoznamo", ali pošto su svi brojevi skupa jedino što mi u prvom trenutku ne bi umeli da ga "prepoznamo", ali pošto su svi brojevi skupa  stavljeni na spisak, i traženi broj je na spisku i ima recimo indeks stavljeni na spisak, i traženi broj je na spisku i ima recimo indeks  . Sada mi lepo pokrenemo naš Generator Broja Van Spiska i u . Sada mi lepo pokrenemo naš Generator Broja Van Spiska i u  -tom koraku on se zaglavi! -tom koraku on se zaglavi![ Bojan Basic @ 14.12.2005. 00:57 ] @
Citat: uranium: Ja samo kažem da je to kad mi stavimo 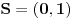 isto kao kad stavimo isto kao kad stavimo 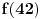 za f-ju za f-ju 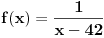 i posle kukamo :"Jao, vidi šta mi se desilo" (opširnije). i posle kukamo :"Jao, vidi šta mi se desilo" (opširnije).Ni približno isto. Funkcija koju si naveo kao primer nije definisana za broj 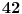 , dok je funkcija o kojoj ovde pričamo savršeno definisana za vrednost , dok je funkcija o kojoj ovde pričamo savršeno definisana za vrednost 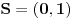 (pod pretpostavkom da je (pod pretpostavkom da je  prebrojiv). prebrojiv).Sledeći tvoj pasus razumem i slažem se u potpunosti sa njim, jedino treba da razrešimo šta znači to zaglavljivanje. Ja tvrdim da kad se zaglavi onda mi kažemo: "E, izgleda smo se negde zaje*ali ranije, i to baš onda kad smo rekli da spisak postoji". Šta ti tvrdiš, zašto je došlo do zaglavljivanja? [Ovu poruku je menjao Bojan Basic dana 14.12.2005. u 01:58 GMT+1] [ uranium @ 14.12.2005. 01:07 ] @
Prvo, već smo videli ( i obučili vrapce
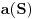 ne može biti definisana u "tački" ne može biti definisana u "tački" 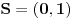 (Doduše, ti bi ovde dodao: "...baš zato što je (Doduše, ti bi ovde dodao: "...baš zato što je  u stvari neprebrojiv" a ja bih, specijalno za ovu priliku, morao da kažem: "Pa ne zanima me zašto. Bitno je da ne može i zaboravimo za trenutak zašto ne može." ) I šta onda? Onaj ko posle toga kaže da postoji u stvari neprebrojiv" a ja bih, specijalno za ovu priliku, morao da kažem: "Pa ne zanima me zašto. Bitno je da ne može i zaboravimo za trenutak zašto ne može." ) I šta onda? Onaj ko posle toga kaže da postoji 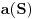 bio bi u potpuno istoj situaciji kao i onaj ko kaže da postoji bio bi u potpuno istoj situaciji kao i onaj ko kaže da postoji 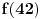 . .A što se tiče zaglavljivanja, sklon sam da kažem da je kriva poslednja pretpostavka koju smo napravili - a to je postojanje traženog broja. [ Nedeljko @ 14.12.2005. 11:53 ] @
Uranim, da pomognem okončanju ove rasprave. Ako prihvatimo ZFC kao formalizaciju matematike, onda je egzistencija odgovarajućeg niza cifara posledica jedne instance aksiome separacije, a postojanje broja
 posledica poredbenog kriterijuma za redove i činjenice da red posledica poredbenog kriterijuma za redove i činjenice da red 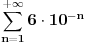 konvergira. To je sve dokazivo sredstvima ZFC. Jedina pretpostavka je bila da dati niz realnih brojeva koji obuhvata sve realne brojeve iz intervala (0,1) postoji. On nije definisan, već je pretpostavljeno da on postoji. Što se tiče logičke pozadine toga, pogledaj teoremu o pravilu C iz teorije predikatskog računa prvog reda. konvergira. To je sve dokazivo sredstvima ZFC. Jedina pretpostavka je bila da dati niz realnih brojeva koji obuhvata sve realne brojeve iz intervala (0,1) postoji. On nije definisan, već je pretpostavljeno da on postoji. Što se tiče logičke pozadine toga, pogledaj teoremu o pravilu C iz teorije predikatskog računa prvog reda.[ Bojan Basic @ 14.12.2005. 12:00 ] @
Ali naprotiv, ja kažem da funkcija jeste definisana u svakoj tački koja se može napisati u obliku spiska, pa i u tački 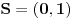 ukoliko bi to bio slučaj. Kako smo definisali funkciju? Tako što smo rekli: "Idi lepo redom po dijagonali i obrći svaku cifru". Zašto ovaj deo do sada isključuje skup ukoliko bi to bio slučaj. Kako smo definisali funkciju? Tako što smo rekli: "Idi lepo redom po dijagonali i obrći svaku cifru". Zašto ovaj deo do sada isključuje skup  ? Ja kažem da uopšte ne isključuje. E tek kad dobijemo tu vrednost koju savršeno možemo da dobijemo jer nigde ne koristimo nikakvo ograničenje u vidu skupa koji smo uzeli, onda gledamo šta se dalje dešava i tek onda se zakucamo. Dakle, definicija funkcije je sasvim u redu. ? Ja kažem da uopšte ne isključuje. E tek kad dobijemo tu vrednost koju savršeno možemo da dobijemo jer nigde ne koristimo nikakvo ograničenje u vidu skupa koji smo uzeli, onda gledamo šta se dalje dešava i tek onda se zakucamo. Dakle, definicija funkcije je sasvim u redu.Citat: uranium: A što se tiče zaglavljivanja, sklon sam da kažem da je kriva poslednja pretpostavka koju smo napravili - a to je postojanje traženog broja. Kao što Nedeljko reče (i usput je objasnio zašto sa formalnog stanovišta), to nigde nismo pretpostavljali, već dokazali. [ uranium @ 14.12.2005. 13:36 ] @
@Nedeljko:
Sa prvim delom tvoje poruke se potpuno slažem (sve vreme sam se i slagao Nisam uspeo da shvatim na koju teoremu misliš. (Pravilo sečenja?!) @Bojan Bašić: Na prvi pogled ti si u pravu i suština našeg neslaganja je samo u tome što ti tvrdiš, da uopšte nije važno kakav spisak je dat. Siguran si da je potpuno izlišno analizirati sadržaj datog spiska, jer je uvek moguće, prateći formalnu proceduru, generisati neki broj van spiska. Ja kažem sledeće: ako si u pravu tj. ako će algoritam uvek dati neki izlaz, onda taj izlaz postoji unapred negde u  (dakle, pre nego što pokrenemo proceduru za njegovo opisivanje) i označimo ga kao i do sada sa (dakle, pre nego što pokrenemo proceduru za njegovo opisivanje) i označimo ga kao i do sada sa 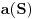 . Dalje, ako sada stavimo da je . Dalje, ako sada stavimo da je 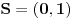 i ti kažeš da će nesumnjivo postojati i ti kažeš da će nesumnjivo postojati 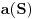 , onda, mora biti , onda, mora biti 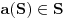 , pa ja kažem pokrenimo onda proceduru i pogledajmo da li ćemo dobiti isto ono što je i trebalo da dobijemo kao izlaz. Pošto prcedura, kako kažeš, radi uvek, dobićemo neki izlaz, koji se na radost svih zainteresovanih, razlikuje od očekivanog i to baš u jednoj cifri! I naravno ti bi sad zaključio da se to desilo zato što spiska u stvari nije ni bilo a ne zato što možda procedura ne može konzistentno da radi sa spiskom koji sadrži sebi pridružen broj... , pa ja kažem pokrenimo onda proceduru i pogledajmo da li ćemo dobiti isto ono što je i trebalo da dobijemo kao izlaz. Pošto prcedura, kako kažeš, radi uvek, dobićemo neki izlaz, koji se na radost svih zainteresovanih, razlikuje od očekivanog i to baš u jednoj cifri! I naravno ti bi sad zaključio da se to desilo zato što spiska u stvari nije ni bilo a ne zato što možda procedura ne može konzistentno da radi sa spiskom koji sadrži sebi pridružen broj...Možda ne bi bilo loše da, koga zanima, pogleda nešto o Ričardovom paradoksu , jer on dobro opisuje moj ugao gledanja na ovu stvar (a to je da ne možemo uvek slepo pratiti formalizme, nego moramo uzimati u obzir i semantiku). Znam da će Nedeljko primetiti da je pomenuti paradoks, paradoks modela i da verovatno i nije paradoks kao i da to ( po običaju [Ovu poruku je menjao uranium dana 14.12.2005. u 14:39 GMT+1] [ Bojan Basic @ 14.12.2005. 14:08 ] @
Citat: uranium: Siguran si da je potpuno izlišno analizirati sadržaj datog spiska, jer je uvek moguće, prateći formalnu proceduru, generisati neki broj van spiska. Siguran sam da je potpuno izlišno analizirati sadržaj datog spiska, jer je uvek moguće, prateći formalnu proceduru, generisati neki broj, tačka. E tek kad završimo sam tim postupkom generisanja broja, onda ćemo proveriti da li je broj van spiska ili nije, do tog momenta nas uopšte ne zanima taj podatak i uopšte se nećemo upucati. Citat: uranium: I naravno ti bi sad zaključio da se to desilo zato što spiska u stvari nije ni bilo a ne zato što možda procedura ne može konzistentno da radi sa spiskom koji sadrži sebi pridružen broj... Vidi, imamo sledeće podatke: 1) Za svaki spisak možemo konstruisati broj; 2) Procedura ne radi konzistentno sa skupom  (tvojim rečima), iliti, u prevodu, nemoguće je konstruisati broj za skup (tvojim rečima), iliti, u prevodu, nemoguće je konstruisati broj za skup  . .Iz 1) i 2) sledi da ne postoji spisak za skup  . .Citat: uranium: Znam da će Nedeljko primetiti da je pomenuti paradoks, paradoks modela i da verovatno i nije paradoks kao i da to ( po običaju :) ) nema nikakve veze sa ovom temom. :) Pošto si ovaj deo ovako lepo sročio nemam više šta da dodam :) [ Nedeljko @ 14.12.2005. 14:27 ] @
Citat: uranium: Možda ne bi bilo loše da, koga zanima, pogleda nešto o Ričardovom paradoksu , jer on dobro opisuje moj ugao gledanja na ovu stvar (a to je da ne možemo uvek slepo pratiti formalizme, nego moramo uzimati u obzir i semantiku). Znam da će Nedeljko primetiti da je pomenuti paradoks, paradoks modela i da verovatno i nije paradoks kao i da to ( po običaju :) ) nema nikakve veze sa ovom temom. :) Izvini uranium, ali sada već moram da te pitam nešto, pre nego što nastavim diskusiju. Da li si ljut na mene, ili misliš da sam ja ljut na tebe, ili misliš da moje učešće nije kostruktivno? Ako je tako, ja ću radije odustati od dalje polemike, nego da ti idem na nerve. [ uranium @ 14.12.2005. 15:27 ] @
@Bojan Bašić:
Citat: Bojan Basic: E tek kad završimo sa tim postupkom generisanja broja, onda ćemo proveriti da li je broj van spiska ili nije, do tog momenta nas uopšte ne zanima taj podatak... Ne razumem zašto bismo ignorisali činjenicu da procedura uvek generiše broj van spiska? Pa zato je i smišljena ta procedura. I kad već sve to znamo, besmisleno je i puštati proceduru za onakav ulaz. Citat: Ja ni ne mogu sasvim da se složim sa 1) (samo nemoj ponovo da me uputiš na ono što ste i ti i Nedeljko napisali, jer sam se sa tim već složio @Nedeljko: Ja sam samo hteo da se malo našalim, jer se do sad na ovom forumu dosta puta desila situacija koju sam pokušao da predvidim I najzad, verujem da se svi slažemo bar oko toga da već duže vreme nije bilo novih argumenata ni protiv a ni u korist dokaza (doduše novih arg. u korist dokaza - nije uopšte ni bilo [ Bojan Basic @ 14.12.2005. 15:45 ] @
Citat: uranium: Ja ni ne mogu sasvim da se složim sa 1) (samo nemoj ponovo da me uputiš na ono što ste i ti i Nedeljko napisali, jer sam se sa tim već složio Jesi ga obrazlagao u više navrata, a ja sam prilikom svakog obrazlaganja verovao da tvoj stav jeste kontradiktoran, pa to verujem i dalje. Nema veze Citat: uranium: I najzad, verujem da se svi slažemo bar oko toga da već duže vreme nije bilo novih argumenata ni protiv a ni u korist dokaza (doduše novih arg. u korist dokaza - nije uopšte ni bilo Naravno, jasno je da je diskusija bila bespoentna (nemam pojma postoji li ova reč u srpskom jeziku, ali razumemo se valjda), pa se slažem s tobom da je možda zaista najbolje ovde stati, svako ko naiđe na ovu diskusiju će moći da pročita celu ovu priču i sam donese svoj sud. Jedino bih još voleo da mi odgovoriš šta se na kraju dogodilo sa onom konstrukcijom koju si pomenuo i ostavio za kasnije, pa se posle nije više pojavljivala? [ uranium @ 14.12.2005. 15:57 ] @
Ostao je jedan strašno bitan deo da se obrazloži (ako je moguće). Ja trenutno stvarno nemam nerava
S tim u vezi pitao bih Nedeljka da li postoji neki snažan logički "alat" koji bi nam omogućio da van svake sumnje ustanovimo šta izaziva kontradikciju. [ Nedeljko @ 14.12.2005. 16:50 ] @
Citat: uranium: Ja sam samo hteo da se malo našalim, jer se do sad na ovom forumu dosta puta desila situacija koju sam pokušao da predvidim :) Izvini ako sam te na bilo koji način uvredio, to mi nije bilo ni na kraj pameti. Ma ne, nisam se ja uvredio. Samo nisam hteo da idem drugima na nerve. Što se tiče Rišarovih "paradoksa", kao i drugih prividnih "paradoksa", u njima ili nije bilo nikakve kontradikcije, već se njima samo tvrdilo nešto što nije u skladu sa ljudskom intuicijom, ili su se njihovom formalizacijom dobijale čuvene teoreme. Formalizacijom prvog od navedenih Rišarovih paradoksa je Gedel dokazao svoju prvu teoremu nepotpunosti. U svakom slučaju, strogim izlaganjem tih "paradoksa" se nije stizalo do logi;ke kontradikcije, ali to nema mnogo veze sa ovom temom (sve si dobro predvideo). Možda bi bilo zgodno otvoriti novu temu za to. Kontradikciju proizvodi to što prebrojivo mnogo cifara 5 i 6 mogu da biram potpuno nezavisno, a bilo kakva promena (na jednoj ili više, konačno ili beskonačno cifara) proizvodi drugi broj. Dovoljno je da se neka dva broja razlikuju na bar jednom mestu, pa da se razlikuju u celini. Stoga mogu da izbegnem sve članove bilo kog prebrojivog podskupa intervala (0,1), jer svakom mogu da pridružim različitu poziciju, pa da od njega vrdnem tačno na toj poziciji. Pošto sam svakom broju pridružio različitu poziciju, a cifre mogu da biram neavisno, dobijeni broj će istovremeno da izvrda sve elemente tog prebrojivog skupa. [ Nedeljko @ 14.12.2005. 17:29 ] @
Jedna od formulacija pravila C glasi ovako:
Neka je 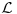 jezik prvog reda i jezik prvog reda i  teorija prvog reda na tom jeziku, teorija prvog reda na tom jeziku, 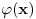 formula jezika formula jezika 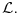 takva da takva da 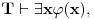 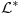 jezik koji se dobija proširivanjem jezika jezik koji se dobija proširivanjem jezika 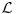 novim simbolom konstante novim simbolom konstante 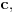 a a 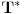 teorija jezika teorija jezika 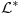 koja se sastoji tačno od aksioma teorije koja se sastoji tačno od aksioma teorije  i još formule i još formule 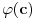 kao jedine dodatne aksiome. Tada za svaku formulu kao jedine dodatne aksiome. Tada za svaku formulu 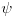 jezika jezika 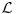 važi važi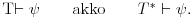 U našem slučaju je 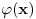 je formula koja tvrdi da je je formula koja tvrdi da je  niz svih realnih brojeva iz intervala (0,1), niz svih realnih brojeva iz intervala (0,1), 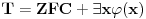 i i 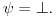 Pošto 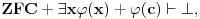 biće i biće i 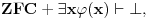 a samim tim i a samim tim i 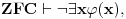 što je i trebalo dokazati. što je i trebalo dokazati.Ovde je 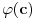 bila dodatna pretpostavka u dokazu, ali bezbedna. Dakle, nije nigde bila dodatna pretpostavka u dokazu, ali bezbedna. Dakle, nije nigde  bilo definisano, već je bilo pretpostavljeno da je bilo definisano, već je bilo pretpostavljeno da je  bilo koji objekat za koji važi bilo koji objekat za koji važi 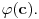 [ uranium @ 14.12.2005. 18:55 ] @
@Nedeljko:
Iskreno se zahvaljujem na svim dodatnim pojašnjenjima. Da li ja grešim ili u jeziku prvog reda nije moguće iskazati osobinu: "  je funkcija sa je funkcija sa 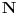 u u  " ? " ?Dalje, bio sam malo neprecizan u vezi sa onim pitanjem u vezi sa logičkim sredstvima utvrđivanja kontradikcije. Mislio sam više na neku tehniku iz Teorije dokaza, koja bi nam omogućila da strogo kontrolišemo tok dokaza i pojavu što pretpostavki, što među-zaključaka, redosleda njihove dalje upotrebe i slično... [Ovu poruku je menjao uranium dana 14.12.2005. u 19:55 GMT+1] [ Nedeljko @ 15.12.2005. 13:17 ] @
Citat: Ovde se radi o izlaganju matematike sredstvima aksiomatske teorije skupova ZFC, koja je teorija I reda. Pogledati teoreme o definicionim ekstenzijama koje šaljem u prilogu. Na primer, neuredjen par 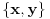 se definiše kao jedinstveni skup kome pripadaju tačno skupovi se definiše kao jedinstveni skup kome pripadaju tačno skupovi  i i 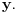 Preciznije, formula Preciznije, formula 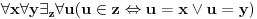 je teorema teorije ZFC, ma možemo uvesti odgovarajući binarni funkcijski znak koji sam označio sa je teorema teorije ZFC, ma možemo uvesti odgovarajući binarni funkcijski znak koji sam označio sa 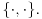 Dalje možeš u teoriji ZFC uvoditi pojam preslikavanja, skupa preslikavanja iz određenog skupa u određeni skup itd. jednostavno prateći uobičajene matematičke definicije. ZFC i ima za cilj da "opravda" ono što matematičari inače rade. Jedno od zasnivanja matematike čine predikatski račun prvog reda na jeziku koji se sastoji samo od jednog binarnog relacijskog znaka 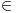 (značii, aksioma i pravila izvođenja tog predikatskog računa) i aksiome ZFC. Tu se može potpuno formalno sprovesti Kantorov dokaz. (značii, aksioma i pravila izvođenja tog predikatskog računa) i aksiome ZFC. Tu se može potpuno formalno sprovesti Kantorov dokaz.[ petarm @ 15.12.2005. 13:32 ] @
Da bi skup (0,1) imao istu moc kao skup realnih brojeva ja bih trebao da pokazem da postoji bijekcija izmedju njih. Na primer ako uzmemo funkciju f(x)=1/(1+ex) (gde mi je x eksponent) i vidim da ako za vrednosti x uzmem skup realnih brojeva jasno vidim da ce mi se za y vrednosti kretati u intervalu (0,1). Kako je nasa f-ja injektivna i sirjektivna ona je bijekcija pa sam pokazao. Ja dalje mogu da zaboravim na skup R i samo da posmatram preslikavanje intervala (0,1) u N. Tako da mene u svemu tome ne zanimaju realni brojevi koji izlaze iz ovog intervala. Posto ne postoji bijekcija izmedju (0,1) i N (a to je vec pokazano na ovom forumu), onda ne postoji ni bijekcija ni izmedju R i N. Pa je skup realnih brojeva neprebrojiv.
[ Bojan Basic @ 15.12.2005. 17:01 ] @
Citat: uranium: Ostao je jedan strašno bitan deo da se obrazloži (ako je moguće). Ja trenutno stvarno nemam nerava :) da se posvetim tome. Ako je od interesa mogu to da postujem u postojećem obliku. Ali pošto ne verujem da je iko osim mene zainteresovan da dodatno ispita šta izaziva kontradikciju u (za mene spornom)dokazu, možda je ipak bolje da to pošaljem ako završim. Ja bih voleo da pošalješ ako je moguće, iako unapred verujem da se i dalje nećemo dogovoriti jednostavno me zanima na kakvu kontrukciju si mislio. [ uranium @ 16.12.2005. 12:19 ] @
Molio bih za još samo malo strpljenja - da pokušam da otklonim sve nedostatke...
[ dust @ 18.12.2005. 03:51 ] @
imam utisak da se sa Kantorovim dijagonalnim postupkom moze dokazati da je skup racionalnih brojeva neprebojiv. Sta mislite?
[ Nedeljko @ 18.12.2005. 11:00 ] @
Ako uspeš da dokažeš da se dijagonalizacijom dobija broj koji je racionalan, izvešćeš kontradikciju iz opšteprihvaćenih matematičkih principa, pa će neki od njih morati da budu odbačeni.
[ Bojan Basic @ 18.12.2005. 16:20 ] @
@dust:
Nemam ništa protiv da ovde izneseš kako bi se to moglo dokazati, pa da diskutujemo. Ja, eto, imam utisak da ne može. [ dust @ 18.12.2005. 22:55 ] @
Ma meni je taj Kantor malo cudan. Sve je pocelo na logici kad smo radili teoremu koja kaze da postoji prebrojiv skup koji zadovoljava aksiome realnih brojeva (naravno ne kaze koji je to skup). A onda sam malo prelistao Kadelburga i nasao dat Kantorov dokaz, i bas mi je izgledalo kao da je moguce zameniti skup realnih brojeva sa skupom racionalnih. Cisto sam hteo da vidim da li neko jos misli slicno, naravno stoji da broj oblika 0.x1x2... ne mora biti racionalan, ali mi se cini da je moguce dobiti racionalan broj dijagonalnim postupkom. Ocigledno nemam dokaz...
[ peddja_stankovic @ 19.12.2005. 07:09 ] @
Nemas garanciju da konstruisan broj ima beskonacan periodicni decimalan zapis sto je potrebno (i dovoljno) da broj bude racionalan
[ dust @ 19.12.2005. 17:19 ] @
Zaboravio sam da se ogradim, kada sam rekao Kantorov dijagonalni postupak, mislio sam na ono sto je dato u Kadelburgovoj knjizi kao dokaz da je skup realnih brojeva neprebojiv. Posto nisam dublje ulazio u teoriju brojeva i teoriju skupova, moje predznanje je malo labavo.
Nemam trenutno Kadelburgovu knjigu kod sebe, ali koliko se secam, ovako bi otprilike zvucao dokaz kad bismo govorili o prirodnim brojevima. Neka su jos prirodni brojevi definisani kao klase ekvivalencije, tako da je broj jedan : 1 01 001 00....001 itd. Sada okrenimo postupak tako da polazimo sa desne strane i uzmimo recimo 10 brojeva. dakle brojevi su: 0000000001 0000000002 0000000003 0000000004 0000000005 0000000006 0000000007 0000000008 0000000009 0000000010 trazimo broj x10x9x8x7x6x5x4x3x2x1 x1 moze biti 9 x2 moze biti 9 . . . x10 moze biti 9 i dakle dobijeni broj moze biti 9999999999 Ako se dobro secam tu se dokaz zavrsava i kaze se eto dobijeni broj se razlikuje od svakog broja u nizu pa je dati skup neprebrojiv. Mozda sam ja nesto prevideo tu, kao sto rekoh imam slabo predznanje iz datih oblasti, ali moj mali mozak nece da prihvati ovakav dokaz. [ Bojan Basic @ 19.12.2005. 20:15 ] @
Dust, to što si ti napisao je upravo ono što je napisao peddja_stankovic negde pri početku teme, i o čemu smo uranium i ja razvukli raspravu naširoko i nadugačko. Predlažem ti da to sve pročitaš, zaista ima dosta informacija, i ako ti ni onda ne bude jasno javi se za dodatno pojašnjenje, ali mislim da trenutno nema smisla ponavljati sve još jednom.
[ dust @ 20.12.2005. 12:42 ] @
pa da, samo sto je prebaceno na prirodne brojeve
[ Bojan Basic @ 20.12.2005. 12:49 ] @
Aha, e pa tako ne može jer svaki prirodan broj ima samo konačno mnogo cifara.
Ne može ni za racionalne, jer ako imaš beskonačno mnogo cifara i dalje nemaš garanciju da je broj koji one određuju racionalan, može biti racionalan ili iracionalan i nemaš načina da to saznaš. [ Farenhajt @ 20.12.2005. 16:35 ] @
Možda ću nešto i lupiti (zarđao sam, izvinjavam se svima koji su u kondiciji), ali zar Kantorovu dijagonalizaciju ne možeš početi proizvoljno daleko od decimalnog zareza? Tj. ako ustanoviš da su ti pokrivene sve moguće kombinacije prvih 5 decimala - od 0,00000xxxx... do 0,99999xxxx... - počećeš dijagonalizaciju od šeste. Ako ti je iscrpljeno prvih milijardu decimala (ili decimale od milionite do milijardite), počećeš od milijardu prve, itd. Pri tome ne možeš kao kontraprimer koristiti konstrukcije na beskonačnim domenima - recimo "a šta ću ako su mi iscrpljene sve decimalne pozicije s parnim indeksom?" - jer prethodno moraš dokazati da se brojevi oblika 0,0x0y0z0t0w... zaista mogu poređati u spisak, tj. da je njihov skup prebrojiv, a to važi akko je prebrojiv skup brojeva oblika 0,xyztw... - dakle, polazni skup.
Dakle, Kantorovoj dijagonalizaciji "opiraće se" konačno mnogo brojeva, što neće uticati na njen rezultat. Sem toga, uranium je svojevremeno napisao: Citat: Ovde se implicira da je broj  jednoznačno određen. Međutim, za svaku cifru "Kantorovog dijagonalnog broja" može se uzeti bilo koja od 9 preostalih cifara (tj. 9 cifara različitih od jednoznačno određen. Međutim, za svaku cifru "Kantorovog dijagonalnog broja" može se uzeti bilo koja od 9 preostalih cifara (tj. 9 cifara različitih od 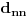 ), te uraniumu sleduje da dokaže da takvih brojeva (dakle, kandidata za "Kantorov dijagonalni broj") može biti najviše prebrojivo mnogo, posle čega bi s pravom mogao tvrditi da procedura može upasti u ćorsokak. Međutim, mislim da u dokazivanju toga neće uspeti. ), te uraniumu sleduje da dokaže da takvih brojeva (dakle, kandidata za "Kantorov dijagonalni broj") može biti najviše prebrojivo mnogo, posle čega bi s pravom mogao tvrditi da procedura može upasti u ćorsokak. Međutim, mislim da u dokazivanju toga neće uspeti.[Ovu poruku je menjao Farenhajt dana 20.12.2005. u 18:02 GMT+1] [ dust @ 21.12.2005. 11:17 ] @
Citat: Bojan Basic: Aha, e pa tako ne može jer svaki prirodan broj ima samo konačno mnogo cifara. Otkud to? [ Bojan Basic @ 21.12.2005. 11:54 ] @
Otkud šta? Svaki prirodan broj ima 100, 1000, 1000000, 1000000000 ili koliko hoćeš cifara, ali ne može da ima beskonačno mnogo.
[ peddja_stankovic @ 23.12.2005. 22:48 ] @
Nesto mi je palo na pamet i mislim da bi ovo moglo da bude znacajno.
Krenucu sa pitanjem prvo. Uzmimo prvo 1 zatim 2 i 3, pa onda 4, 5, 6, 7, pa onda 8, 9, 10, 11, 12, 13, 14, 15, itd, itd. Dakle uzeo sam 20 brojeva zatim 21 brojeva zatim 22 brojeva zatim 23 brojeva itd itd. Nastavimo taj proces u beskraj. Pitanje: Da li ce mi za taj postupak biti dovoljno prirodnih brojeva? Ako je odgovor NE, tada pada popularan dokaz da je harmonijski red divergentan Ako je odgovor DA moglo bi se pokazati da je (0,1) prebrojiv. I treca opcija negde gresim ili nesto ne znam? [Ovu poruku je menjao peddja_stankovic dana 23.12.2005. u 23:50 GMT+1] [Ovu poruku je menjao peddja_stankovic dana 24.12.2005. u 00:15 GMT+1] [ Bojan Basic @ 23.12.2005. 23:53 ] @
Citat: peddja_stankovic: Pitanje: Da li ce mi za taj postupak biti dovoljno prirodnih brojeva? Ne razumem u kom smislu "dovoljno". Ukoliko je pitanje da li ćemo moći da uzimamo beskonačno mnogo tura, onda je odgovor da. Citat: peddja_stankovic: Ako je odgovor DA moglo bi se pokazati da je (0,1) prebrojiv. Ipak ne vidim kako bi ovo moglo da se pokaže. Može li malo pojašnjenje ideje? [ peddja_stankovic @ 24.12.2005. 02:42 ] @
Uzmimo binarni zapis brojeva od 0 do 1.
0.0110110110001010110011010101010101001010111100101..... je neki broj iz (0,1). Obratimo paznju samo na dva broja: 0.0 i 0.1 Sada obratimo paznju na 0.00 0.01 0.10 0.11 Ima ih 4. Sada na 0.000 0.001 0.010 0.011 0.100 0.101 0.110 0.111 Ima ih 8 itd itd. Ponavljajuci ovaj postupak u beskraj dobicemo sve varijacije sa ponavljanjem sa beskonacno mnogo cifara. Njih ima 2+4+8+16+.... , upravo koliko i brojeva iz moje prethodne poruke. Znaci mozemo prebrojati sve realne brojeve iz (0,1). U literaturi i pise da continuum = 2alef0 gde je alef0 "broj" prirodnih brojeva. [ uranium @ 24.12.2005. 07:31 ] @
Ovim postupkom je prebrojan samo jedan podskup racionalnih brojeva iz intervala
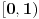 - tj. onih sa konačnim binarnim zapisom. Na primer, ni jedan racionalan broj oblika - tj. onih sa konačnim binarnim zapisom. Na primer, ni jedan racionalan broj oblika 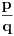 , , 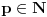 , ,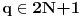 , , 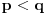 neće biti "uhvaćen" ovim postupkom. neće biti "uhvaćen" ovim postupkom.Sledeća primedba nije upućena Peđi. Što se tiče zapisa 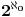 treba imati u vidu: treba imati u vidu: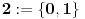 oznaka 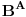 je oznaka za skup svih preslikavanja iz je oznaka za skup svih preslikavanja iz  u u  ako prihvatimo aksiomu izbora, onda je 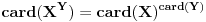 . .A motivaciju bi trebalo tražiti u sledećem: Svakom binarnom zapisu realnog broja iz intervala 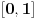 možemo pridružiti karakterističnu funkciju nekog podskupa možemo pridružiti karakterističnu funkciju nekog podskupa 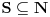 . Naravno, ovde su mogući i ekvivalentni zapisi ( npr. . Naravno, ovde su mogući i ekvivalentni zapisi ( npr. 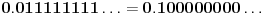 ) a problemi koje to izaziva lako se mogu prevazići, jer takvih brojeva (tj. odgovarajućih podskupova) ima samo prebrojivo mnogo, pa njihovo uklanjanje ne menja kardinalnost skupa ) a problemi koje to izaziva lako se mogu prevazići, jer takvih brojeva (tj. odgovarajućih podskupova) ima samo prebrojivo mnogo, pa njihovo uklanjanje ne menja kardinalnost skupa 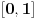 (odnosno skupa (odnosno skupa 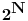 ). ).Dakle, izgleda da je kombinatorika na beskonačnim skupovima - vrlo nezgodna (ali i uzbudljiva) disciplina [Ovu poruku je menjao uranium dana 24.12.2005. u 09:36 GMT+1] [ uranium @ 24.12.2005. 09:07 ] @
Tek sad sam primetio da je poruka koju je poslao Farenhajt bila menjana.
Citat: Farenhajt: Ovde se implicira da je broj  jednoznačno određen. Međutim, za svaku cifru "Kantorovog dijagonalnog broja" može se uzeti bilo koja od 9 preostalih cifara (tj. 9 cifara različitih od jednoznačno određen. Međutim, za svaku cifru "Kantorovog dijagonalnog broja" može se uzeti bilo koja od 9 preostalih cifara (tj. 9 cifara različitih od 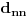 ), te uraniumu sleduje da dokaže da takvih brojeva (dakle, kandidata za "Kantorov dijagonalni broj") može biti najviše prebrojivo mnogo, posle čega bi s pravom mogao tvrditi da procedura može upasti u ćorsokak. Međutim, mislim da u dokazivanju toga neće uspeti. ), te uraniumu sleduje da dokaže da takvih brojeva (dakle, kandidata za "Kantorov dijagonalni broj") može biti najviše prebrojivo mnogo, posle čega bi s pravom mogao tvrditi da procedura može upasti u ćorsokak. Međutim, mislim da u dokazivanju toga neće uspeti.Čak i kad se ograničimo na izbor samo dve cifre (  i i 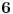 ) dobijamo da je ) dobijamo da je 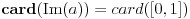 , (svakom broju iz , (svakom broju iz 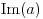 odgovara jedan binaran zapis broja iz odgovara jedan binaran zapis broja iz 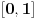 ) dakle sve i da hoću, zaista nema šanse da dokažem da je skup kandidata najviše prebrojiv a da to ne bude kao u ovoj šali: ) dakle sve i da hoću, zaista nema šanse da dokažem da je skup kandidata najviše prebrojiv a da to ne bude kao u ovoj šali: "There is no logical foundation of mathematics, and Gödel has proved it!" [ peddja_stankovic @ 24.12.2005. 18:11 ] @
Cim sam poslao ideju posumljao sam da sam ustvari dokazivao broj racionalnih brojeva. Ipak verujem da se tu moze mnogo toga iscackati. Pa zato "natrag u laboratoriju" kao sto rece Pera Kojot Super Genije.
[ Bojan Basic @ 24.12.2005. 18:40 ] @
Kao što reče uranium, nisu čak ni racionalni brojevi nego samo neki od njih - u postupku nije uhvaćen nijedan broj sa beskonačno mnogo binarnih decimala.
Lično, ne verujem da se može mnogo toga iščačkati jer bi to značilo da istovremeno možemo dokazati neko tvrđenje i njegovu negaciju, a iz toga bi sledilo da aksiome koje su u upotrebi nizu konzistentne, i samim tim pada skoro celokupna dosadašnja matematika - strašno, nije li? :) Ipak, u svakom slučaju sam raspoložen da pročitam nove ideje pa možemo diskutovati i o njima. [ Nedeljko @ 24.12.2005. 19:48 ] @
[ uranium @ 24.12.2005. 20:12 ] @
[ Nedeljko @ 24.12.2005. 21:53 ] @
Pa i ako je prazan, kakve to veze ima? Zar prazan skup nije dobro definisan? Šta fali praznom skupu?
Ponavljam, to što si napisao je definicija stepenovanaj kardinala, i kao takva se ne dokazuje. To je samo jedna konvencija o korišćenju alternativnog zapisa za nešto zašta već postoji zapis. Drugo, skup  je prazan ako i samo ako je je prazan ako i samo ako je 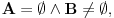 i to nema nikakve veze sa aksiomom izbora. Ako je i to nema nikakve veze sa aksiomom izbora. Ako je  prazan, omnda postoji tačno jedna funkcija koja slika skup prazan, omnda postoji tačno jedna funkcija koja slika skup  u skup u skup 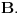 To je takozvana prazna funkcija, pa je skup To je takozvana prazna funkcija, pa je skup  neprazan jer sadrži jedan element - praznu funkciju. Ako li je pak neprazan jer sadrži jedan element - praznu funkciju. Ako li je pak 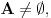 onda postoji neko onda postoji neko  (ovo nije upotreba aksiome izbora), pa postoji i funkcija koja preslikava sve elemente skupa (ovo nije upotreba aksiome izbora), pa postoji i funkcija koja preslikava sve elemente skupa  (ako ih ima) u element (ako ih ima) u element 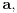 odakle ponovo skup odakle ponovo skup  nije prazan. nije prazan.Aksioma izbora je ekvivalentna sa nepraznošću proizvoda beskonačne familije nepraznih skupova u opštem slučaju. Postoje posebni slučajevi kada se nepraznost beskonačnog proizvoda nepraznih skupova može dokazati i bez nje. [ uranium @ 24.12.2005. 22:43 ] @
Ne, nema ništa loše u tome da ponekad taj skup bude i prazan
Jedina "briga" je bila u tome da u opštem slučaju znamo da postoje objekti sa kojima radimo (u ovom slučaju članovi skupa 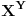 ). Znam da na jednom mestu Đuro Kurepa, pomalo nonšalantno kaže da je pitanje praznog skupa duboko pitanje, ali verujem da ćemo se složiti da nije osnovni rezultat to da sve lepo radi ako je ). Znam da na jednom mestu Đuro Kurepa, pomalo nonšalantno kaže da je pitanje praznog skupa duboko pitanje, ali verujem da ćemo se složiti da nije osnovni rezultat to da sve lepo radi ako je 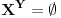 . . Inače, spornu teoremu je dokazao Friedrich Hartogs, koji je izgleda - gle ironije - proučavao ZF bez aksiome izbora. Ja sam skup 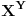 i shvatio kao Dekartov proizvod familije nepraznih skupova i shvatio kao Dekartov proizvod familije nepraznih skupova 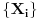  gde je za svako gde je za svako 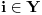 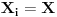 , tako da je i pretpostavka o aksiomi izbora sasvim na mestu (kao što se i sam slažeš u pretposlednjoj rečenici). , tako da je i pretpostavka o aksiomi izbora sasvim na mestu (kao što se i sam slažeš u pretposlednjoj rečenici).S druge strane, zaista ne znam za te posebne slučajeve (a pogotovu da li je 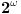 jedan od njih)- ali moram priznati da mi sve to zvuči vrlo uzbudljivo i voleo bih da saznam više o tome (jel možeš da daš neku (pristupačnu) referencu?) jedan od njih)- ali moram priznati da mi sve to zvuči vrlo uzbudljivo i voleo bih da saznam više o tome (jel možeš da daš neku (pristupačnu) referencu?)U stvari sad mi se čini da preko aksiome stepena i aksiome beskonačnosti zaista možemo (bez upotrebe aksiome izbora) da dobijemo da je 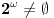 . .[Ovu poruku je menjao uranium dana 25.12.2005. u 00:20 GMT+1] [ Nedeljko @ 25.12.2005. 01:51 ] @
Možeš li da konstruišeš bar jednu funkciju koja slika
 u u 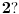 Jedan od načina je konstrukcija konstantne funkcije. Kada god izbornu funkciju možeš da konstruišeš, ili na bilo koji drugi način da dokažeš da ona postoji, ne moraš se pozivati na aksiomu izbora. Jedan od načina je konstrukcija konstantne funkcije. Kada god izbornu funkciju možeš da konstruišeš, ili na bilo koji drugi način da dokažeš da ona postoji, ne moraš se pozivati na aksiomu izbora.Posmatraj familiju svih nepraznih podskupova skupa realnih brojeva. Njen proizvod bez aksiome izbora može biti i prazan. U ovom slučaju ne možeš zadati način da se iz proizvoljnog nepraznog podskupa skupa realnih brojeva izdabere po jedan njegov element. Na koju si Hartogsovu teoremu mislio. Ja znam za onu da za svaki skup  postoji skup koji se može injektivno preslikati u njega, a koji se može dobro urediti, kao i za onu da iz zakona trihotomije (ili dihotomije) sledi aksioma izbora. postoji skup koji se može injektivno preslikati u njega, a koji se može dobro urediti, kao i za onu da iz zakona trihotomije (ili dihotomije) sledi aksioma izbora.Ono što mi smeta u vezi sa aksiomom izbora je sledeće: Ako radimo u neaksiomatskoj TS, onda ne koristimo nikakve aksiome teorije skupova, pa ni aksiomu izbora. Ukoliko pak radimo u aksiomatskoj TS, onda se moramo pozivati na svaku aksiomu koju koristimo. Zašto stalno isticati primenu aksiome izbora, a ne isticati upotrebu drugih aksioma TS? [ Bojan Basic @ 25.12.2005. 10:26 ] @
Citat: Nedeljko: Ono što mi smeta u vezi sa aksiomom izbora je sledeće: Ako radimo u neaksiomatskoj TS, onda ne koristimo nikakve aksiome teorije skupova, pa ni aksiomu izbora. Ukoliko pak radimo u aksiomatskoj TS, onda se moramo pozivati na svaku aksiomu koju koristimo. Zašto stalno isticati primenu aksiome izbora, a ne isticati upotrebu drugih aksioma TS? Ovo je malo offtopic, ali moram da iskomentarišem. Nedeljko, potpuno si u pravu, i mene to strašno nervira. Ježim se kad vidim rešenje nečega, i na kraju komentar: "E, sad smo rešili pomoću aksiome izbora, ajd' sad neko da reši bez nje". Ili, druga varijanta: "Dokazati to i to bez primene aksiome izbora". Mis'im stvarno, ako su se ljudi već dogovorili da prelome i da je prihvate takvu kakva je, zašto se još uvek protežu filozofiranja? Eto, sad možemo da se vratimo na temu. [ Nedeljko @ 25.12.2005. 13:32 ] @
Razmatranje nekih matematičkih pitanja u svetlu aksiomatske teorije skupova bez aksiome izbora ili uz ostale aksiome teorije skupova + neka zamena za aksiomu izbora (nekim slabijim ili jačim oblikom) imaju smisla, kao i diskutovanje nekih drugih jakih aksioma teorije skupova. Međutim, to može imati smisla samo u aksiomatskoj teoriji skupova kada se tačno zna koje se aksiome koriste. Ali, onda se poziva na sve te aksiome onda kada se koriste, a ne samo na jednu.
Takođe, nemoj misliti da su mišljenja matematičara oko toga koji su osnovni matematički principi opravdani nepodeljena. Dopusti da razni ljudi imaju razna mišljenja. Međutim, smatram da sve to treba da bude matematički dosledno, a ne da se stvara lažan utisak da u matematici postoji samo jedna aksioma, i da tu aksiomu možemo koristiti ili ne koristiti u smislu da postoje stavovi koji slede iz te jedne aksiome, kao i drugi stavovi koji slede ni iz čega. [ uranium @ 25.12.2005. 13:59 ] @
offtopic:
Meni se čini da je potpuno nevažno da li će se neko eksplicitno pozvati na neku aksiomu ili ne, to je stvar i ukusa i konteksta rasprave. Detaljnom analizom upotrebljenih argumenata se (verovatno) može ustanoviti da li bi isti zasključak važio i u bilo kojoj poznatoj aksiomatskoj teoriji skupova ili ne. E sad, uopšte mi nije jasno zašto bi aksioma izbora imala isti status kao i ostale aksiome (ako zanemarimo formalnu stranu). Nisam nikad čuo za teoriju skupova bez npr. aksiome unije. Znači, mislim da uvek treba naglasiti upotrebu samo onih stavova oko kojih postoje podeljena mišljenja. @Bojan Bašić: Slobodno briši ovo pre nego što... [Ovu poruku je menjao uranium dana 25.12.2005. u 15:01 GMT+1] [ Bojan Basic @ 25.12.2005. 21:53 ] @
Citat: Nedeljko: Razmatranje nekih matematičkih pitanja u svetlu aksiomatske teorije skupova bez aksiome izbora ili uz ostale aksiome teorije skupova + neka zamena za aksiomu izbora (nekim slabijim ili jačim oblikom) imaju smisla, kao i diskutovanje nekih drugih jakih aksioma teorije skupova. Međutim, to može imati smisla samo u aksiomatskoj teoriji skupova kada se tačno zna koje se aksiome koriste. Citat: uranium: Detaljnom analizom upotrebljenih argumenata se (verovatno) može ustanoviti da li bi isti zasključak važio i u bilo kojoj poznatoj aksiomatskoj teoriji skupova ili ne. Sa ovim se, naravno, slažem. Ono što sam pisao u prošloj poruci nije se odnosilo na izučavanje nekog problema sa formalnog stanovišta, već na rešavanje problema bez spuštanja na tako niske nivoe. Da navedem i primer koji mi je trenutno pao na pamet. Pitanje je da li Košijeva funkcionalna jednačina ima rešenje različito od identičke funkcije. Odgovor, kakav sam video na većini mesta, je: "Da, ukoliko prihvatimo aksiomu izbora". Ja bih na postavljeno pitanje odgovorio sa da, bez suvišnih komentara, jer aksioma izbora jeste prihvaćena. To i dalje ne sprečava (a i ne bi trebalo da sprečava) formaliste da gledaju šta bi bilo kad bi bilo, ali smatram da je prilikom ovakvog pitanja postavljenog u ovakvom kontekstu drugi deo odgovora savršeno bespotreban. Citat: Nedeljko: Dopusti da razni ljudi imaju razna mišljenja. Pre nekog vremena pričali smo o hipotezi kontinuuma, koja se meni lično sviđa i smatram da bi trebala da bude prihvaćena. Vudinu se, primera radi, ne sviđa i smatra da bi njena negacija trebala da bude prihvaćena (ovo "sviđa" i "ne sviđa" govorim više metaforično, bez zalaženja u razloge za i protiv). Zamislimo da se jednoga dana postigne konsenzus da bude po njegovom. E, od tog momenta ću ja, prilikom rešavanja zadataka, koristiti negaciju hipoteze kontinuuma, bez obzira na to što se moje mišljenje razlikuje od opšteprihvaćenog. Zaključak, svakako da ne branim da razni ljudi imaju razna mišljenja, ali mislim da formalistima treba prepustiti da se igraju aksiomama dok ostale ne treba da je briga za to već samo treba da slede prihvaćene principe iako eventualno mogu da se ne slažu sa njima. Citat: uranium: offtopic: Nisam nikad čuo za teoriju skupova bez npr. aksiome unije. Evo, možeš i sam da napraviš jednu. Recimo, uzmi neku već postojeću i izbaci aksiomu unije, nazovimo ovo npr. Uraniumova aksiomatika. Sad mene zanima zašto bi, recimo, ZF bez C bila bitnija od Uraniumove aksiomatike. Pretpostavljam da ćeš reći da je to zbog toga što ova prva ima nekog smisla a druga nema, ali tu sledi deo gde se verovatno ne slažemo. Ja kažem da za formaliste (koliko li sam puta upotrebio ovu reč) sve ima podjednakog smisla dok za ostatak matematičkog sveta jedna i samo jedna teorija ima smisla dok ostale nemaju, ili bi bar tako trebalo da bude. [ Nedeljko @ 25.12.2005. 23:03 ] @
Citat: uranium: Znači, mislim da uvek treba naglasiti upotrebu samo onih stavova oko kojih postoje podeljena mišljenja. Hajde uranijum, koliko znaš ljudi koji iskreno dovode u pitanje aksiomu izbora. Više od 99,9% onih koji je svaki put prozivaju, uopšte je ne dovode u pitanje, već je prozivaju samo zbog onih manje od 0,1% koji sumnjaju u nju. Kada se drugačije ne kaže, podrazumeva se da se koriste principi koji se mogu opravdati u ZFC. Ako neko izvodi nešto iz nekih drugih principa, jačih ili slabijih, neka napiše šta koristi od aksioma i nema problema. [ uranium @ 26.12.2005. 00:51 ] @
Citat: Nedeljko:Kada se drugačije ne kaže, podrazumeva se da se koriste principi koji se mogu opravdati u ZFC. Znači, hoćeš da kažeš da nije bilo pogrešno što sam naveo i pretpostavku o 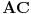 , nego je to bio pleonazam (pa je ipak pogrešno sa stilskog stanovišta). , nego je to bio pleonazam (pa je ipak pogrešno sa stilskog stanovišta). Pošto je rasprava krenula vrlo "ozbiljnim" tokom, nadam se da nećete imati ništa protiv da prekucam nekoliko citata: prvo jedan "protivan" mom stavu: Citat: A. K. Dewdney: The axiom gets its name not because mathematicians prefer it to other axioms. a onda jedan za Nedeljka: Citat: Jerry Bona: The Axiom of Choice is obviously true, the well-ordering principle obviously false, and who can tell about Zorn's lemma? E sad ozbiljno: poznato je da ako pretpostavimo  onda dobijamo da postoje skupovi neuporedivi u smislu kardinalnosti - a to bi moglo biti od interesa za neke varijante pokušaja obaranja onog dokaza (ako se još neko seća šta je bila tema onda dobijamo da postoje skupovi neuporedivi u smislu kardinalnosti - a to bi moglo biti od interesa za neke varijante pokušaja obaranja onog dokaza (ako se još neko seća šta je bila tema [ Nedeljko @ 26.12.2005. 15:55 ] @
Citat: uranium: Znači, hoćeš da kažeš da nije bilo pogrešno što sam naveo i pretpostavku o , nego je to bio pleonazam (pa je ipak pogrešno sa stilskog stanovišta) Hoću da kažem da je to jedna izlizana moda lišena svakog smisla. Ili ćemo se dosledno pozivati na sve aksiome TS, ili nećemo ni na jednu. Osim toga Citat: Nedeljko: smatram da sve to treba da bude matematički dosledno, a ne da se stvara lažan utisak da u matematici postoji samo jedna aksioma, i da tu aksiomu možemo koristiti ili ne koristiti u smislu da postoje stavovi koji slede iz te jedne aksiome, kao i drugi stavovi koji slede ni iz čega. Da li sam napokon jasan? Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|