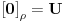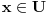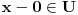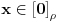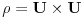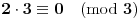Par pitanja iz Binarnih relacija

[ maximus_1 @ 09.12.2005. 14:24 ] @

1.)Problem1
Na skupu brojeva A = {1,2,3,4,5,6,7,8,9} zadana je relacija p = {(x, y): xy je
kvadrat nekog prirodnog broja}.

To znam:
p = {(1,1), (1,4), (1,9), (2,2), (2,8), (3,3), (4,1), (4,4), (4,9), (5,5), (6,6),
(7,7), (8,2), (8,8), (9,1), (9,4), (9,9)}

to su elementi relacije. Njih nije teško ispisati
Problem je kad treba ispisati sve klase ekvivalencije(kvocijentni skup)?
Kako se to radi? Koliko ja znam to su brojevi koji se ponavljaju pa bi bilo:

[1]_p= {1,4,9}, [2]_p= {2,8}, [3]_p= {3}, [4]_p= {1,4,9}, [5]_p= {5}, [6]_p= {6}, [7]_p= {7},[8]_p= {2,8},[9]_p= {1,4,9}.

No u rješenjima nema ni [4]_p, ni [8]_p, ni [9]_p.č
Je li to zato što se u njima ponavlja {1,4,9)?

2.)Problem2:
Definiramo relaciju p pravi podskup UxU na sljedeÄ�i naÄ�in apb <=> a - b
element iz U.

Odredite klasu ekvivalencije broja 1.2
To zaista ne znam ni započet!
Kako se to radi?

3.) Treći problem
Zadana je matrica A tipa (3,3) sa a_ij=ij(mod3). Ispiši matricu A?
kako se to radi?

Znam ja ispisat matricu ali me muči ovo mod 3. Ako je a_ij=a₁₁ tj. a₁₁=1(mod3). Kako ću onda napisat čemu je to jednako ako nemam broj s lijeve straner jednakosti?

[ uranium @ 09.12.2005. 15:09 ] @

1. Stvar je samo u tome što važi :

, dakle nije bitno koji element klase ćeš istaći kao predstavnika - svi elementi su "ravnopravni". Ista priča i za 2 i 8.

2. Izgleda da nisi napisao šta je to

. I još bitnije: nije jasno da li se traži relacija ekvivalencije ili ne.

Ako je odgovor "ne", onda se ne sme upotrebljavati termin klasa ekvivalencije broja 1.2
A ako je odgovor "da" onda je zadatak loše postavljen:

(zbog refleksivnosti relacije

i verovatno

).
Sada je jasno da je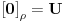

, jer za svako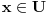

važi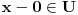

tj.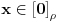

.

Međutim, iz tranzitivnosti sledi da je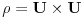

, a to je suprotno postavci!

3. Ne razumem u čemu je problem. Nekoliko primera:

U preseku 2. vrste i 3. kolone upisaćeš 0, zato što je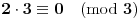

.

U preseku 1. vrste i 2. treće kolone upisaćeš 2, zato što je

.

itd.

_{[Ovu poruku je menjao uranium dana 09.12.2005. u 16:23 GMT+1]}

[ maximus_1 @ 09.12.2005. 15:38 ] @

Hvala, puno.
Dakle Problem jedan mi je jasan ako se ponavljaju isti izrazi s desne strane jednakosti onda se ne pišu.

Problem 2 nije ni meni postavljeno šta je U.

Problem 3:

Citat:

U preseku 2. vrste i 3. kolone upisaćeš 0, zato što je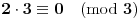

Je li upisulem nula zato što je 2*3 djeljivo sa 3 ili ne?
Tamo gdje nije djeljivo samo upišem taj broj

_{Bojan Bašić: uopšte ne shvatam poentu citata koji sam obrisao. U svakom slučaju, pročitaj Pravilnik.}

_{[Ovu poruku je menjao Bojan Basic dana 09.12.2005. u 16:50 GMT+1]}

[ uranium @ 09.12.2005. 16:10 ] @

Zadatak 3.

Upisuješ ostatak pri deljenju sa 3 (ako je broj deljiv sa 3 ostatka nema, pa ćeš upisati 0).