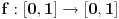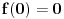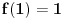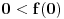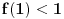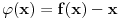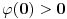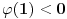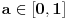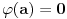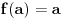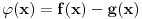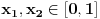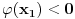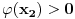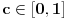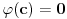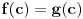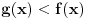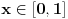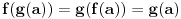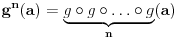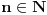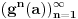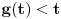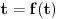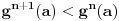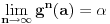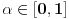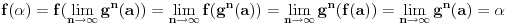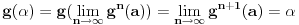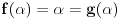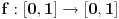
Lema 1. Svaka neprekidna funkcija ima fiksnu tačku.
Dokaz.
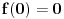
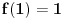
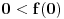
Ako je ili tvrđenje je dokazano, u suprotnom važi i .
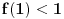
Uvedimo pomoćnu neprekidnu funkciju .
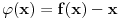
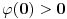
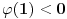
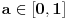
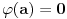
Vidimo da je a , pa na osnovu Bolcano-Košijeve teoreme o međuvrednosti postoji tačka za koju je , tj. .

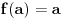
Sada možemo da krenemo sa rešavanjem postavljenog zadatka.

Uvedimo pomoćnu neprekidnu funkciju .
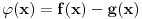
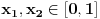
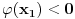
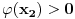
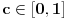
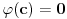
Ako bi postojale tačke za koje bi važilo i , onda bi postojala i tačka za koju važi tj. .
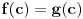
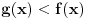
Zato, ostaje da razmotrimo slučaj kada je pomoćna f-ja konstantnog znaka. Neka su funkcije označene tako da važi za svako .

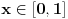
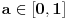
Na osnovu Leme 1. postoji takva da .
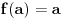
Zbog komutativnosti datih funkcija dobijamo da je .
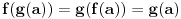
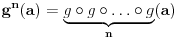
Dakle, dobili smo zanimljivu osobinu: ako je fiksna tačka f-je , onda je fiksna tačka i za svako .

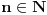
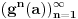
Niz je ograničen i opadajući. Evo zašto je i opadajući.
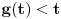
Za svaku fiksnu tačku f-je važi: (jer je )
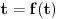
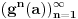
Pošto su sve tačke niza fiksne za f-ju , dobijamo da je .


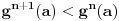
Znači taj niz konvergira.

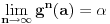
Drugim rečima za neko .

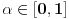
Vidimo da je fiksna tačka funkcije , jer je .
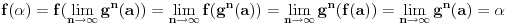
Ali, je fiksna tačka i f-je , jer je .

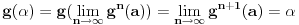
To je to, .

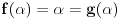
_{[Ovu poruku je menjao uranium dana 12.12.2005. u 09:09 GMT+1]}