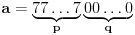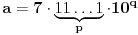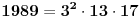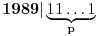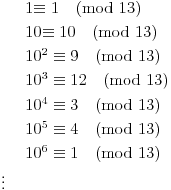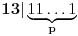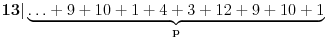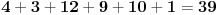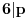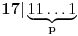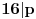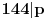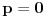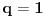[ pirgos_madden @ 10.12.2005. 20:21 ] @
| Dakle kako ovo resiti, na nivou ucenika 6. razreda osnovne: 7777...77000...000 je broj koji ima p sedmica i q nula. Naci p i q tako da broj bude deljiv sa 1989. Ja sam dobio za p=144 (ili bilo koji umnozak od 144) ali me zanima kako se ovo moze dobiti na nacin prihvatljiv ucenicima 6. razreda osnovne skole gde je zadatak bio i zadat (mada iskreno... nisam bas 100% siguran ni da je 144 pravo resenje :). Hvala na pomoci ! |