Prvi sam resila.
Povodom drugog zadatka:
To je deo nekog zadatka.
Ovaj polinom ponistava broj
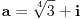
Treba naci minimalni polinom od

nad
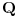
Inace, Mathcad kaze da je ovaj nerastavljiv.
E, sad, posto za polinom ne pali ni Ajzenstajn, a probala sam i
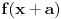
(bezuspesno),
a deluje mi strasno da pretpostavim da je rastavljiv, pa da ispitujem slucajeve,
mozda moze i nesto drugo:
posto je
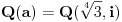
vazi
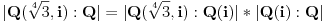
I sad ovaj
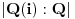
je 2 a kako da pokazem da je
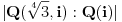
upravo 4
(jer to ce biti dosta da zakljucim da je bas f minimalni)?
Povodom treceg:
a)
Skup
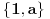
gde je
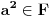
jeste linearno nezavisan (lako se pokaze).
Takodje, skup svih linearnih kombinacija od 1 i a tj
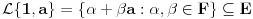
ocigledno.
Ali kako da pokazem da je i obrnuto, tj da nema elemenata iz E koji nisu generisani sa 1 i a?
Ako uzmem neku drugu bazu za E pa probam da "napakujem" - ne uspeva.
b)
Gledajte smer S(L) = S(K)

postoji F-izomorfizam
Ja nigde ne koristim pretpostavku S(L) = S(K) , a napravim preslikavanje
koje je F-izomorfizam
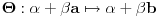
gde je
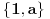
baza od L a
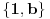
baza od K
Dakle, sta da radim?