Stavi u x1 i x2 resenja te kvadratne jednacine i pomnozi ono sto si napisao.

npr.ak imaš jednačinu

x^2+2x-3=0

njena rješenja su -3 i 1

ak sad to gore ubaciš.....dobijaš... 1*(x+3)(x-1)=x^2-x+3x-3=x^2+2x-3 i to je to

Jasno je meni to, i da X1 i X2 trba da budu cinioci broja 3(u tvom primeru) To se moze potvrditi kada se pomnozi ali zasto je tako?

da probamo ovako:

x1+x2=-b/a => b=-a(x1+x2)
x1*x2= c/a => c= a(x1*x2)

ax^2+bx+c=ax^2-a(x1+x2)x+a(x1*x2)=a[x^2-(x1+x2)x+x1*x2]=a[x^2-x1*x-x2*x+x1*x2]=a[x(x-x1)-x2(x-x1)]=a(x-x1)(x-x2)

sto je i trebalo dokazati ;)

Nauka nam govori kako se nesto radi, ali ne i zasto.

<sub>Bojan Bašić: Uklonjeni suvišni [b] i [sub] tagovi.

[Ovu poruku je menjao Bojan Basic dana 28.12.2005. u 17:53 GMT+1]</sub>

Ovo shto si ti napisao je sasvim uredu, ti si pomocu Vietovih formula dosao do izraza koji sam trazila, ali mi smo Vietove formule izvodili iz trazenog izraza a(x-x1)(x-x2) tako da je to shto si ti uradio samo obrnut proces!!!!

E bash je svrha nauke da nam kaze ZASTO!!!!!!!!!

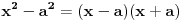
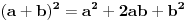
Da li ti je jasno zašto se razlika kvadrata piše kao ? Da li ti je jasno zašto se kvadrat binoma piše Trebalo bi, pošto to spada u najosnovnije rastavljanje polinoma na činioce, i radi se u osnovnoj školi.

Ako je to jasno, možemo dalje (u toku izvođenja stavljene su fusnote s objašnjenjima):






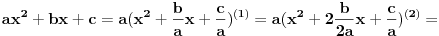
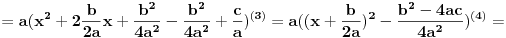
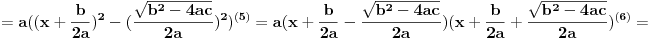
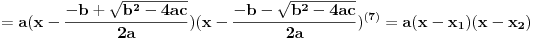
Objašnjenja:
(1) Izvukli smo ispred zagrade
(2) Srednji član u zagradi pomnožili smo i podelili sa 2, jer nam je ideja da napravimo kvadrat binoma
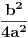
(3) Unutar zagrade smo dodali i oduzeli i tako nam prva tri člana postaju kvadrat binoma
(4) Izdvojili smo kvadrat binoma, a preostale članove sredili u jedan razlomak
(5) Drugi član u zagradi napisali smo kao kvadrat da bismo dobili razliku kvadrata
(6) Rastavili smo izraz kao razliku kvadrata
(7) Sredili smo razlomke

Dakle, na kraju dobijamo upravo ono što nam treba. Ako ima još nešto nejasno, slobodno pitaj.

_{[Ovu poruku je menjao Farenhajt dana 28.12.2005. u 11:45 GMT+1]}

E pa hvala ti jer mi je sve sad jasno.(nisu ti trebale one fusnote). Nama je profesorka samo rekla da rezultat. Ja vise volim da znam zasto je tako. Jos je dnom ti hvala shto si se potrudio!!!!

Dala vam je samo gotove izraze za rešenja kvadratne jednačine, a nije ih izvodila? Zanimljivo... (Možda je ne plaćaju dovoljno da bi i to radila )

Naravno da je ne placaju dovoljno ( na zalost) !!!! Bolje bi radila da joj je malo veca plata! Ja najvise volim matematiku!!! Zao mi je shto nisam upisala matematicku gimnaziju nego sam upisala ovu jadnu i bednu gimnaziju!!!

Izvini, postavicu dva glupa pitanja:

1. Koja je to glupa gimnazija ?
2. Da li si pokusala da procitas nesto u udzbeniku matematike ?

1. svaka gimnazija u koju se upisu ucenici koji ni osnovne stvari nisu naucili u osnovnoj skoli.... ocito je profesorka smatrala da im je pretesko za razumjeti samo izvodjenje formula (i da je to samo gubljenje vremena), pa ih je samo napisala i rekla da nauce napamet
2. naravno da nije otvorila, jer to sto su neki pisali u ovoj temi, od rijeci do rijeci isto to pise i u knjizi!!!!!