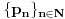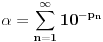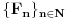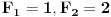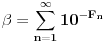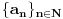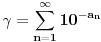[ Farenhajt @ 22.12.2005. 22:46 ] @
|
[ Bojan Basic @ 10.03.2006. 02:41 ] @
Najpre navodim jednu teoremu [1].
Teorema: Neka je 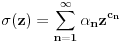 , gde je , gde je 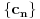 monotono rastući niz prirodnih brojeva, a monotono rastući niz prirodnih brojeva, a 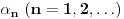 su nenula racionalni brojevi. Neka je su nenula racionalni brojevi. Neka je 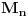 najmanji zajednički imenilac brojeva najmanji zajednički imenilac brojeva  . Pretpostavimo da važi . Pretpostavimo da važi 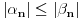 za sve dovoljno velike za sve dovoljno velike  , gde su , gde su 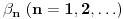 realni brojevi koji zadovoljavaju realni brojevi koji zadovoljavaju 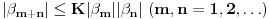 za neku konstantu za neku konstantu  . Pretpostavimo dalje da je . Pretpostavimo dalje da je 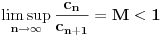 , , 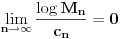 . Tada je . Tada je 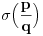 transcendentan za sve cele brojeve transcendentan za sve cele brojeve 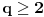 i i  koji zadovoljavaju koji zadovoljavaju 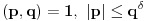 , gde je , gde je  dat pozitivan broj za koji važi dat pozitivan broj za koji važi 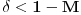 . .Najpre ćemo odabrati vrednosti tako da možemo primeniti Teoremu u situaciji koju imamo. Neka je: 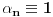 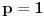 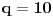 Možemo uzeti 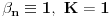 , pa , pa 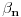 ispunjava traženi uslov i zaista važi ispunjava traženi uslov i zaista važi 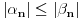 za dovoljno veliko za dovoljno veliko  (štaviše, važi za sve (štaviše, važi za sve  ). Kako pri ovako odabranim vrednostima važi ). Kako pri ovako odabranim vrednostima važi 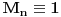 , sledi da je , sledi da je 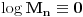 , pa je ispunjeno i , pa je ispunjeno i 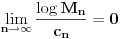 . Dakle, možemo formulisati posledicu koja delimično odgovara na pitanje broj 3. . Dakle, možemo formulisati posledicu koja delimično odgovara na pitanje broj 3.Posledica: Neka je 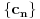 monotono rastući niz prirodnih brojeva za koji važi monotono rastući niz prirodnih brojeva za koji važi 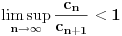 . Tada je broj . Tada je broj 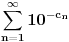 transcendentan. transcendentan.Primetimo da iz Posledice trivijalno sledi da je odgovor na pitanje broj 2 potvrdan, s obzirom na to što je 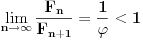 , gde je , gde je  zlatni presek. zlatni presek.Nažalost, ovaj pristup nam neće mnogo pomoći za pitanje broj 1 jer je malo verovatno da je 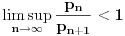 budući da bi to oborilo mnoge hipoteze za koje se veruje da su tačne, kao što je na primer čuvena Twin Prime Conjecture. budući da bi to oborilo mnoge hipoteze za koje se veruje da su tačne, kao što je na primer čuvena Twin Prime Conjecture.[1] Zhu,Yao Chen & Ren, Jian Hua, The transcendence of the values of certain gap series at rational points, J. Northwest Univ. 12 (1982), no. 4, 1–8. Potpuno sam svestan da ovo nije odgovor kakav bi iko želeo da vidi. S druge strane, tema stoji već duže vreme bez ikakvog napretka pa smatram da je makar i ova priča bolja od ćutanja. [Ovu poruku je menjao Bojan Basic dana 09.06.2006. u 14:25 GMT+1] [ Bojan Basic @ 28.03.2006. 10:54 ] @
Citat: Bojan Basic: Nažalost, ovaj pristup nam neće mnogo pomoći za pitanje broj 1 jer je malo verovatno da je 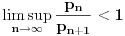 budući da bi to oborilo mnoge hipoteze za koje se veruje da su tačne, kao što je na primer čuvena Twin Prime Conjecture. budući da bi to oborilo mnoge hipoteze za koje se veruje da su tačne, kao što je na primer čuvena Twin Prime Conjecture.Ne samo da je malo verovatno nego se moze dokazati da vazi 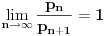 . .Neka je 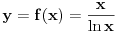 . Trazimo inverznu funkciju ovoj funkciji. Primetimo da je, dalje, . Trazimo inverznu funkciju ovoj funkciji. Primetimo da je, dalje, 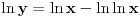 , a posto vazi , a posto vazi 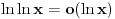 onda imamo onda imamo 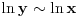 . Iz toga sledi da je . Iz toga sledi da je 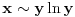 . Primenimo ovo na poznatu asimptotsku relaciju . Primenimo ovo na poznatu asimptotsku relaciju 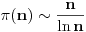 . Posto je . Posto je 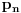 ( (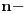 ti prost broj) funkcija inverzna funkciji ti prost broj) funkcija inverzna funkciji 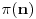 , vazi , vazi 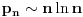 . Sada se lako dobija da je . Sada se lako dobija da je 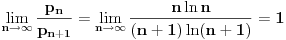 . .[Ovu poruku je menjao Bojan Basic dana 09.04.2006. u 20:18 GMT+1] [ Nedeljko @ 14.05.2023. 20:59 ] @
Potvrdan odgovor na 3, a samim tim i na 1 sledi iz sledećeg iskaza:
Citat: Svaki algebarski broj je racionalan ili normalan. Ovaj iskaz nije dokazan. Predstavlja hipotezu koja je najverovatnije tačna. Pomenuti zadaci iz prve poruke za sada nisu rešeni (ne samo na ovom forumu, nego uopšte u matematici). Navodim definicije: A) Za kompleksan broj  kažemo da je algebarski ako postoji barem jedan polinom kažemo da je algebarski ako postoji barem jedan polinom 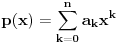 takav da su svi od brojeva takav da su svi od brojeva  celi (odnosno racionalni) brojevi, od koji je barem jedan različit od nule i pri čemu je celi (odnosno racionalni) brojevi, od koji je barem jedan različit od nule i pri čemu je 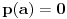 . U suprotnom se za kompleksan broj . U suprotnom se za kompleksan broj  kaže da je transcedentan. kaže da je transcedentan.B) Neka je  realan broj takav d aje realan broj takav d aje 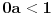 i neka je i neka je 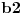 ceo broj. Tada postoji tačno jedan beskonačan niz celih brojeva ceo broj. Tada postoji tačno jedan beskonačan niz celih brojeva 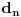 za koji važi za koji važi 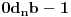 i i 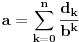 i pri čemu nisu svi elementi niza počev od nekog jednaki i pri čemu nisu svi elementi niza počev od nekog jednaki 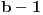 . Tada za niz . Tada za niz 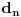 kažemo da je decimalni razvoj broja kažemo da je decimalni razvoj broja  u standardnom pozicionom sistemu sa osnovom u standardnom pozicionom sistemu sa osnovom  . .C) Za realan broj  se kaže da je normalan ako za svaki ceo broj se kaže da je normalan ako za svaki ceo broj 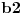 važi sledeće: važi sledeće:Neka je  jedinstveni ceo broj za koji važi jedinstveni ceo broj za koji važi 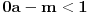 i neka je i neka je 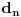 decimalni razvoj u standardnom pozicionom sistemu sa osnovom decimalni razvoj u standardnom pozicionom sistemu sa osnovom  . Tada za svaki ceo broj . Tada za svaki ceo broj  takav da je takav da je 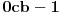 važi da mu relativna frekvencija pojavljivanja teži ka važi da mu relativna frekvencija pojavljivanja teži ka 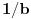 . Drugim rečima, ako je . Drugim rečima, ako je 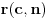 broj pojavljivanja broja broj pojavljivanja broja  u nizu u nizu  (dakle, na prvih (dakle, na prvih  mesta), onda je mesta), onda je 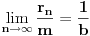 . .Ako iracionalan realan broj u svom decimalnom razvoju sadrži samo cifre 0 i 1, onda on nije normalan jer je frekvencija pojavljivanja cifre 2 jednaka nuli, pa prema navedenoj hipotezi ne može biti algebarski, odnosno transcedentan je. [ Bojan Basic @ 17.05.2023. 20:52 ] @
Citat: Nedeljko: Pomenuti zadaci iz prve poruke za sada nisu rešeni (ne samo na ovom forumu, nego uopšte u matematici). Imaš neku referencu zašto smatraš da je zadatak 2 otvoren problem? Jer po onome što sam napisao u svom prvom odgovoru (pre malo više od 17 godina [ Nedeljko @ 18.05.2023. 18:34 ] @
Da, taj jeste rešen. Mislio sam na preostale.
[ Nedeljko @ 18.05.2023. 21:45 ] @
BTW, LaTeX sa ovog foruma ne podržava komande \leqslant i \geqslant, nego se moraju koristiti \leq i \geq, pa u vezi s tim ispravljam greške koje su se potkrale u formulama.
Potvrdan odgovor na 3, a samim tim i na 1 sledi iz sledećeg iskaza: Citat: Svaki algebarski broj je racionalan ili normalan. Ovaj iskaz nije dokazan. Predstavlja hipotezu koja je najverovatnije tačna. Pomenuti zadaci iz prve poruke za sada nisu rešeni (ne samo na ovom forumu, nego uopšte u matematici). Navodim definicije: A) Za kompleksan broj  kažemo da je algebarski ako postoji barem jedan polinom kažemo da je algebarski ako postoji barem jedan polinom 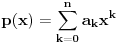 takav da su svi od brojeva takav da su svi od brojeva  celi (odnosno racionalni) brojevi, od koji je barem jedan različit od nule i pri čemu je celi (odnosno racionalni) brojevi, od koji je barem jedan različit od nule i pri čemu je 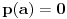 . U suprotnom se za kompleksan broj . U suprotnom se za kompleksan broj  kaže da je transcedentan. kaže da je transcedentan.B) Neka je  realan broj takav d aje realan broj takav d aje 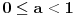 i neka je i neka je 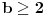 ceo broj. Tada postoji tačno jedan beskonačan niz celih brojeva ceo broj. Tada postoji tačno jedan beskonačan niz celih brojeva 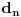 za koji važi za koji važi 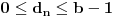 i i 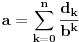 i pri čemu nisu svi elementi niza počev od nekog jednaki i pri čemu nisu svi elementi niza počev od nekog jednaki 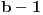 . Tada za niz . Tada za niz 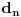 kažemo da je decimalni razvoj broja kažemo da je decimalni razvoj broja  u standardnom pozicionom sistemu sa osnovom u standardnom pozicionom sistemu sa osnovom  . .C) Za realan broj  se kaže da je normalan ako za svaki ceo broj se kaže da je normalan ako za svaki ceo broj 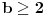 važi sledeće: važi sledeće:Neka je  jedinstveni ceo broj za koji važi jedinstveni ceo broj za koji važi 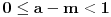 i neka je i neka je 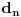 decimalni razvoj u standardnom pozicionom sistemu sa osnovom decimalni razvoj u standardnom pozicionom sistemu sa osnovom  . Tada za svaki ceo broj . Tada za svaki ceo broj  takav da je takav da je 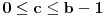 važi da mu relativna frekvencija pojavljivanja teži ka važi da mu relativna frekvencija pojavljivanja teži ka 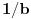 . Drugim rečima, ako je . Drugim rečima, ako je 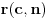 broj pojavljivanja broja broj pojavljivanja broja  u nizu u nizu  (dakle, na prvih (dakle, na prvih  mesta), onda je mesta), onda je 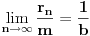 . .Ako iracionalan realan broj u svom decimalnom razvoju sadrži samo cifre 0 i 1, onda on nije normalan jer je frekvencija pojavljivanja cifre 2 jednaka nuli, pa prema navedenoj hipotezi ne može biti algebarski, odnosno transcedentan je. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|