[ past_love2001 @ 23.12.2005. 22:18 ] @
| Pokazati dva eksplicitno iracionalna broja a, b tako da je a^b racionalno |
|
[ past_love2001 @ 23.12.2005. 22:18 ] @
[ uranium @ 23.12.2005. 22:26 ] @
[ Farenhajt @ 24.12.2005. 12:00 ] @
[ Nedeljko @ 24.12.2005. 19:52 ] @
@Farenhajt
To što si napisao jeste dokaz da traženi brojevi postoje, ali ne i rešenje zadatka koji glasi "Naći brojeve a i b takve da...". Ako se traži samo dokaz postojanja, onda je ovo OK. Ako se traži da se ti elementi i nađu, onda nisi napisao šta je a, a šta b. [ Farenhajt @ 25.12.2005. 02:27 ] @
[ Farenhajt @ 30.12.2005. 21:59 ] @
[ uranium @ 30.12.2005. 23:29 ] @
[ Farenhajt @ 31.12.2005. 00:17 ] @
Jel' to da malo vežbamo ugneždene logaritme u TeX-u?
A konto toga: Šta kaže teoretičar brojeva kad padne u vodu? Log-log-log-log-log... [ uranium @ 31.12.2005. 01:20 ] @
Ha, ha!
 ko nije shvatio štos neka klikne ovde Citat: Farenhajt: Jel' to da malo vežbamo ugneždene logaritme u TeX-u? Izgleda da imaš neka drugačija rešenja od onih koje sam ja imao u vidu, mada, priznajem da sam se nadao da ću usput videti kako se u 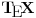 -u piše "up right ellipsis". -u piše "up right ellipsis". [ Farenhajt @ 31.12.2005. 01:23 ] @
Proširimo li tvoju ideju (pod oznakom
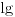 podrazumeva se podrazumeva se 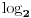 , radi sažetosti) i uzmemo li u obzir da je , radi sažetosti) i uzmemo li u obzir da je 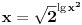 , imamo: , imamo: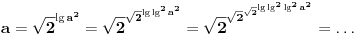 , i tako , i tako  puta, gde se puta, gde se  mora odabrati dovoljno veliko da bi ugneždeni logaritmi ostali definisani. mora odabrati dovoljno veliko da bi ugneždeni logaritmi ostali definisani.A tebi ostavljam dokaz da je 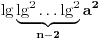 iracionalan broj, kao i diskusiju o dovoljno velikom iracionalan broj, kao i diskusiju o dovoljno velikom  Šalu na stranu - lakši rezultat dobija se na sledeći način: Slično kao maločas, lako se dokazuje da je 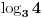 iracionalan, a pri tome imamo da je iracionalan, a pri tome imamo da je 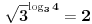 . Sada možemo pisati: . Sada možemo pisati: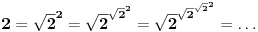 Postupak nastavljamo koliko nam puta treba, a završnu dvojku u eksponentu pišemo kao Postupak nastavljamo koliko nam puta treba, a završnu dvojku u eksponentu pišemo kao 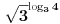 . .Dakle, jedna moguća  -torka koja daje rezultat -torka koja daje rezultat  glasi glasi 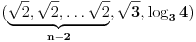 . .[ uranium @ 31.12.2005. 01:39 ] @
[ Farenhajt @ 31.12.2005. 01:51 ] @
Hoćemo li sad tražiti
 -torke gde su svi brojevi po parovima različiti? -torke gde su svi brojevi po parovima različiti? (I mislim da ne razumem ovo da si imao varijantu da su svi osim poslednjeg koren iz 2 - to rešenje sam i ja postovao [Ovu poruku je menjao Farenhajt dana 31.12.2005. u 03:06 GMT+1] [ uranium @ 31.12.2005. 02:09 ] @
[ Farenhajt @ 31.12.2005. 02:27 ] @
Lepo
[ uranium @ 31.12.2005. 02:41 ] @
Nemam pojma - što i nije čudno u ovo doba "dana"
Ali u svakom slučaju imamo posla sa nekim rođakom Ackermann-ove funkcije - pa ko voli da računa... [ Farenhajt @ 31.12.2005. 02:45 ] @
[ uranium @ 31.12.2005. 02:56 ] @
Sigurno svi osim Nedeljka
[ Farenhajt @ 31.12.2005. 03:02 ] @
Da, da... video sam ovaj thread, ali ga smetnuh s uma
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|