[ Farenhajt @ 24.12.2005. 12:52 ] @
| Može li neko da navede adicione formule za trećinu ugla? (Može i link.) Hvala. |
|
[ Farenhajt @ 24.12.2005. 12:52 ] @
[ uranium @ 24.12.2005. 13:28 ] @
Verovatno nisam dobro razumeo šta se traži (jer ne vidim vezu između adicije i trećine ugla - šta bi se tu čemu dodavalo?), ali možda je u pitanju ovo:
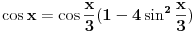 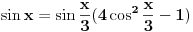 Evo kako je to dobijeno: 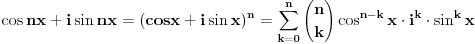 Zatim razdvojimo realni i imaginarni deo i dobijemo odvojene formule za obe funkcije. Pošto formule važe za svako  možemo da stavimo možemo da stavimo 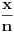 umesto umesto  . .[ Farenhajt @ 24.12.2005. 14:21 ] @
1. Mene učili (svojevremeno) da se u trigonometriji sve transformacije funkcija zbira uglova, razlike uglova, dvostrukog ugla, polovine ugla, proizvoda funkcija u zbir, zbira funkcija u proizvod združeno (i sažeto) zovu adicione formule. (Možda se terminologija promenila? Ili takvih termina ima neprebrojivo mnogo?
2. Hvala na ponuđenim formulama (umem i sam da ih izvedem), ali su one upravo obratne od onoga što meni treba - dakle, izraziti funkcije trećine ugla preko funkcija celog ugla (a ne ono što je gore navedeno). [Ovu poruku je menjao Farenhajt dana 24.12.2005. u 15:22 GMT+1] [ uranium @ 24.12.2005. 16:32 ] @
Citat: Farenhajt: Hvala na ponuđenim formulama (umem i sam da ih izvedem) Nisam ni sumnjao Citat: uranium: Verovatno nisam dobro razumeo šta se traži Znači nisam hteo da te uvredim (izvinjavam se što se to desilo), već samo verujem da će uvek biti i onih koji prvi put vide te formule... Sad kad sam shvatio Sigurno ne kao neku racionalnu f-ju sinusa (odnosno kosinusa). Naravno, jasno mi je da ovo poslednje samo po sebi ne znači puno, jer imamo sasvim lepe formule za polovinu ugla koje takođe nisu racionalne f-je sinusa (odnosno kosinusa) (ali s druge strane - polovljenje ugla pomoću šestara i lenjira je uvek moguće). Postoji jedna stara tema - koja je na moju veliku žalost ostala nedovršena (i čini mi se sa nekim greškama), ali mislim da je od interesa za rešenje ovog problema. [ Farenhajt @ 24.12.2005. 22:01 ] @
Dragi uraniume, nema nikakve nesuglasice
Elem: Citat: uranium: s obzirom na negativno rešenje problema trisekcije ugla, u kom obliku tražimo rešenje? Nadam se da ćeš se složiti da je sledeći izraz tačan: 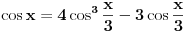 (dobija se sasvim lako iz prvog izraza koji si napisao u svojoj prvoj poruci). Sada ja pitam: Pošto je po 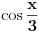 ovo kubna, te stoga i rešiva jednačina, zanima me da li je neko negde nekad "ispešačio" to rešenje i napisao ga u obliku koji obuhvata konačan broj zbirova, razlika, proizvoda, količnika, kvadratnih korenova i kubnih korenova realnih brojeva i trigonometrijskih funkcija od ovo kubna, te stoga i rešiva jednačina, zanima me da li je neko negde nekad "ispešačio" to rešenje i napisao ga u obliku koji obuhvata konačan broj zbirova, razlika, proizvoda, količnika, kvadratnih korenova i kubnih korenova realnih brojeva i trigonometrijskih funkcija od  . .Pitanje zaista nema reperkusija na (ne)izvodljivost trisekcije ugla pomoću lenjira i šestara, jer ne tražimo geometrijsku konstrukciju kubnog korena (za koju, dao bog, znamo da je nemoguća [Ovu poruku je menjao Farenhajt dana 24.12.2005. u 23:01 GMT+1] [ uranium @ 24.12.2005. 22:17 ] @
[ Bojan Basic @ 24.12.2005. 23:30 ] @
Citat: Čini mi se da grešiš. Ono što mi tražimo je 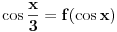 . Zapravo, treba izraziti . Zapravo, treba izraziti 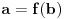 iz iz 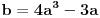 , a to je obično rešavanje kubne jednačine. , a to je obično rešavanje kubne jednačine.@Farenhajt: Ovo može da odradi bilo koji matematički program, mada sumnjam da ćeš dobiti bilo šta upotrebljivo. Ja sam trenutno kod roditelja i nažalost nije mi nijedan pri ruci, ali ako ti već nemaš verujem da će neko od članova foruma pokrenuti i javiti nam rezultat, a ukoliko do sutra uveče niko ne napiše izraz napisaću ga ja kad se domognem svog kompjutera. [ uranium @ 24.12.2005. 23:55 ] @
Evo šta kaže kompjuter:
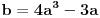 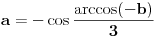 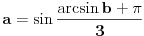 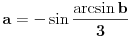 i ako sad stavimo 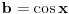 dobijamo neke f-je dobijamo neke f-je 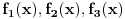 i pogledamo grafike f-ja 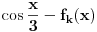 . .Dobijamo sličicu [att_img] Dakle, rešenje bi se zaista moglo dobiti ali kao unija nekih restrikcija pomenutih funkcija. Meni u ovom trenutku uopšte nije jasno zašto se to desilo 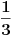 dana dana Bojane, jel imaš neko objašnjenje za ovo? [Ovu poruku je menjao uranium dana 25.12.2005. u 01:16 GMT+1] [ Farenhajt @ 25.12.2005. 00:12 ] @
Na ovom sajtu nađoh:
"George Joachim (1514—1576), known as Rheticus [...] found the formulae for the sines of the half and third of an angle in terms of the sine of the whole angle." Dakle, biće da je to urađeno još u 16. veku, ali se te formule slabo pominju zbog skoro pa neprebrojivosti [Ovu poruku je menjao Farenhajt dana 25.12.2005. u 01:13 GMT+1] [ Farenhajt @ 25.12.2005. 03:17 ] @
Hmmmm...
Rešavanjem jednačine 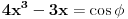 , gde je , gde je  parametar, dobija se... čik pogodite šta: parametar, dobija se... čik pogodite šta: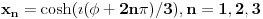 ... a svi znamo čemu je to jednako. ... a svi znamo čemu je to jednako.Začarani krug - otkud? Pitam se, pitam se... @uranium: Pođeš li, na primer, od 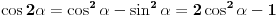 , stavljanjem , stavljanjem 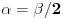 dobijaš dobijaš 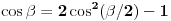 . Odatle prostom transformacijom dobijaš staru dobru formulu . Odatle prostom transformacijom dobijaš staru dobru formulu 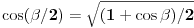 , a primenjeni postupak praktično se svodi na "rešavanje (kvadratne) jednačine po , a primenjeni postupak praktično se svodi na "rešavanje (kvadratne) jednačine po 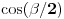 ". ".[ Bojan Basic @ 25.12.2005. 22:18 ] @
Citat: uranium: Bojane, jel imaš neko objašnjenje za ovo? :) Probaću. Programi koji rešavaju jednačine imaju neki algoritam za to (ko bi rekao :)). E sad, kakav je algoritam koji je koristio tvoj program ili jedan od mojih programa koji je dao isti rezultat (Derive 6) ne znam, ali očigledno prilikom rešavanja kubnih jednačina koristi trigonometrijske funkcije verovatno radi jednostavnijeg oblika. S druge strane, neki drugi program ima neki drugi algoritam koji koristi samo radikale, i korišćenjem jednog takvog (Mathematica 5.0) zaista možemo dobiti eksplicitnu vrednost, pri čemu moramo paziti i na ograničenja, jer od tri rešenja kubne jednačine samo jedno nas zanima. To baš i nije jednostavno zapisati, ali koga zanima neka pokrene program pa vidi. [ Farenhajt @ 25.12.2005. 23:56 ] @
Citat: Bojan: To baš i nije jednostavno zapisati, ali koga zanima neka pokrene program pa vidi Možeš li formulu konvertovati u PDF ili TXT format, pa okačiti, ili poslati privatnom porukom, ili nekako...? [ uranium @ 26.12.2005. 00:08 ] @
[ Farenhajt @ 26.12.2005. 01:24 ] @
[ uranium @ 26.12.2005. 12:59 ] @
[ Farenhajt @ 26.12.2005. 14:33 ] @
U drugoj formuli, faktor uz prvi sabirak iznosi
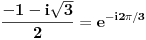 , a uz drugi (kad znak minus između dva sabirka "uvučeš" u sam sabirak) iznosi , a uz drugi (kad znak minus između dva sabirka "uvučeš" u sam sabirak) iznosi 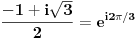 , tako da posle sređivanja dobijaš izraz , tako da posle sređivanja dobijaš izraz 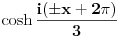 . Analogno i treća. Dakle, nominalno dobijamo 3 različite vrednosti za . Analogno i treća. Dakle, nominalno dobijamo 3 različite vrednosti za 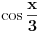 , koje, naravno, daju 6 mogućih vrednosti za sam ugao u intervalu , koje, naravno, daju 6 mogućih vrednosti za sam ugao u intervalu 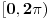 . .Poenta je u tome što u 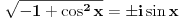 treba uzeti samo one kombinacije znakova koje daju realnu vrednost za treba uzeti samo one kombinacije znakova koje daju realnu vrednost za 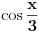 . .I da, pravilno si shvatio šta me muči [Ovu poruku je menjao Farenhajt dana 26.12.2005. u 15:54 GMT+1] [ Farenhajt @ 26.12.2005. 16:57 ] @
Evo, da ispešačim kubnu jednačinu:
Jednačinu 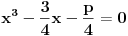 , gde je , gde je 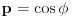 parametar, rešavamo direktno Vijetovom smenom parametar, rešavamo direktno Vijetovom smenom 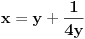 , jer je faktor uz član , jer je faktor uz član  jednak nuli. Posle sređivanja dobijamo: jednak nuli. Posle sređivanja dobijamo: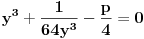 . .Smenom 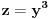 dobijamo kvadratnu jednačinu dobijamo kvadratnu jednačinu 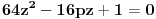 , čija su rešenja , čija su rešenja 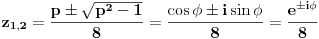 . .Ako sa 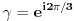 i i 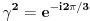 označimo kompleksne kubne korene iz 1, uslov označimo kompleksne kubne korene iz 1, uslov 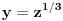 za za 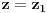 daće nam daće nam 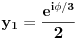 , , 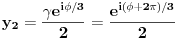 , , 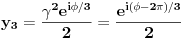 , a za , a za 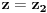 dobijamo dobijamo 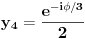 , , 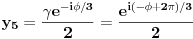 , , 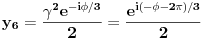 . .Zamenom vrednosti 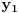 u Vijetovu smenu, dobijamo u Vijetovu smenu, dobijamo 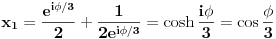 , a iz , a iz 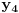 dobijamo dobijamo 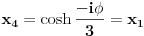 . Na isti način, iz . Na isti način, iz 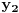 i i 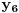 dobijamo dobijamo 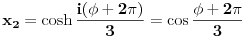 , a iz , a iz 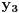 i i 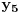 dobijamo dobijamo 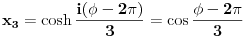 . .Dakle, gde smo bili - nigde, šta smo radili - ništa... [Ovu poruku je menjao Farenhajt dana 26.12.2005. u 18:50 GMT+1] [ uranium @ 26.12.2005. 17:42 ] @
[ Farenhajt @ 26.12.2005. 20:50 ] @
[ uranium @ 26.12.2005. 22:38 ] @
Evo u prilogu jednog lako shvatljivog rešenja (?!) koje je izbacila Mathematica 5.2
Ne bih da širim defetizam, ali... [ Farenhajt @ 26.12.2005. 22:57 ] @
Nažalost, nemam Mathematicu, pa ne mogu da se razaberem u ovom sitnom vezu (a ni "plagovanje" u TeX na ovom forumu ne uspeva...) Imaš li neku JPG verziju? Recimo preko PrintScreen, pa Paste u neki grafički program?
[ uranium @ 26.12.2005. 23:10 ] @
Ovo je skoro pola prve strane (od 16). Prvi par rešenja staje na jednu stranicu. Ako misliš da ima svrhe, mogao bih da pokušam da to spakujem u nekoliko sličica...
[ Farenhajt @ 26.12.2005. 23:29 ] @
Mislim, stvarno... od ovoga može i da se umre
Doduše, ovo pola izraza deluje mi žešće nesređeno, na prvi pogled, ali zaista nemam ambicija da to ručno peglam... U svakom slučaju, kopka me šta li je to Rheticus uradio - nisam uspeo da nađem nikakav dalji izvor na Netu. [ uranium @ 27.12.2005. 00:02 ] @
I mene kopka
Ali, možda postoji jedno razočaravajuće objašnjenje. Rheticus je pravio numeričke tablice svih osnovnih trigonometrijskih funkcija, pa je možda reč o nekoj numeričkoj aproksimaciji koja je radila dovoljno dobro... [ Farenhajt @ 27.12.2005. 00:37 ] @
A konto ovog autputa iz Mathematike: Uoči da je, na primer - odmah na početku, prvi razvijeniji imenilac -
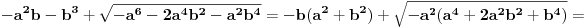 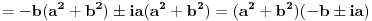 , a ceo taj izraz stoji pod kubnim korenom. Dakle, ni Mathematica ne ume da izbegne eksponencijalno korenovanje kompleksnog broja, po svoj prilici, a očito se UOPŠTE ne zamlaćuje sređivanjem. , a ceo taj izraz stoji pod kubnim korenom. Dakle, ni Mathematica ne ume da izbegne eksponencijalno korenovanje kompleksnog broja, po svoj prilici, a očito se UOPŠTE ne zamlaćuje sređivanjem.Mada slutim da bi morala postojati neka funkcija koja sređuje dati izraz? Recimo polinom ili polinomijalni razlomak... [Ovu poruku je menjao Farenhajt dana 27.12.2005. u 01:46 GMT+1] [ uranium @ 27.12.2005. 00:54 ] @
Evo, malo sam ga sredio
[Ovu poruku je menjao uranium dana 27.12.2005. u 01:58 GMT+1] [ Farenhajt @ 27.12.2005. 01:24 ] @
Sređuj, sređuj... pa mi se javi kad bude "realizam"
[ uranium @ 27.12.2005. 01:49 ] @
[ uranium @ 27.12.2005. 02:44 ] @
Sad sam već ozbiljno počeo da sumnjam da je tražena formula postojala.
[att_img] Eto, Rheticus-ova formula nam je bila sve vreme pred nosom (znao si je još u srednjoj školi Tako da kada isteraš ovaj tvoj problem do kraja, potrudićemo se da formula dobije naziv: Farenhajtov identitet. A i ako ne isteraš, ostaje nam svakako identitet 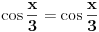 , pa ćemo njega zvati tim imenom. , pa ćemo njega zvati tim imenom. Ja sam već ranije rezervisao za sebe onaj sa 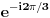 [Ovu poruku je menjao uranium dana 27.12.2005. u 08:41 GMT+1] [ Farenhajt @ 27.12.2005. 05:51 ] @
[ Farenhajt @ 27.12.2005. 19:52 ] @
Elem, šalu na stranu. Na ovom sajtu (ovog puta daleko ozbiljnijem
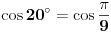 . Ovde citiram odgovor: . Ovde citiram odgovor:Citat: Dakle, izgleda da mi je posao od samog početka bio osuđen na propast, tj. da je uranium zaista bio na pravom tragu kad je 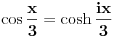 proglasio Farenhajtovim identitetom proglasio Farenhajtovim identitetom [ uranium @ 27.12.2005. 21:31 ] @
Gojko Kalajdžić Algebra
U poglavlju Raširenja polja, kraj odeljka Konstruktibilni brojevi daje deo odgovora na tvoje pitanje, ali to je otprilike ono što sam već napisao u drugom (po redu) postu. Nadam se da neću povrediti autorska prava ako parafraziram jedan delić: Krenemo od onog što već znamo 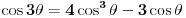 . Ako uzmemo . Ako uzmemo 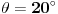 iz prethodne formule sledi da broj iz prethodne formule sledi da broj 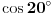 poništava polinom poništava polinom 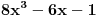 , a pošto je on nerastavljiv nad , a pošto je on nerastavljiv nad 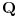 , onda je minimalni polinom broja , onda je minimalni polinom broja 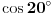 stepena 3. stepena 3.E sad se lepo pozovemo na teoremu koja kaže da minimalni polinom konstruktibilnog broja mora biti stepen dvojke - i time smo dobili da je 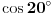 nekonstruktibilan. nekonstruktibilan.Ostaje da primetimo još i to da je skup konstruktibilnih brojeva 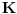 potpolje od potpolje od 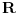 - i dobili smo da ako formula postoji, ona ne može biti racionalna f-ja (sa koeficijentima iz - i dobili smo da ako formula postoji, ona ne može biti racionalna f-ja (sa koeficijentima iz 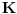 ) sinusa/kosinusa celog ugla (jer npr. ) sinusa/kosinusa celog ugla (jer npr. 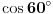 je konstruktibilan broj). je konstruktibilan broj).[ Farenhajt @ 27.12.2005. 23:50 ] @
Delimičan odgovor, da - ali i dalje ne vidim implikaciju od nekonstruktibilnosti do analitičke neizrazivosti pomoću konačne kombinacije sabiranja, oduzimanja, množenja, deljenja i korenovanja realnih brojeva i realnih funkcija realnog argumenta
 . .Recimo, ako je data duž  , onda duž , onda duž  koja zadovoljava uslov koja zadovoljava uslov 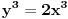 nije konstruktibilna (ako ja dobro shvatam značenje tog termina), ali jeste izraziva kao nije konstruktibilna (ako ja dobro shvatam značenje tog termina), ali jeste izraziva kao 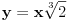 . .Dakle, moje pitanje eksplicitno glasi: Zašto se u izrazu za 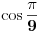 ili, uopšteno, u izrazu za ili, uopšteno, u izrazu za 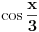 kada kada 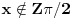 moramo zadovoljiti nerazrešenim kubnim korenima kompleksnih brojeva? moramo zadovoljiti nerazrešenim kubnim korenima kompleksnih brojeva?[Ovu poruku je menjao Farenhajt dana 28.12.2005. u 02:03 GMT+1] [ uranium @ 28.12.2005. 01:31 ] @
Dakle, skup konstruktibilnih brojeva
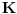 je zatvoren za operacije sabiranja, oduzimanja, množenja, deljenja, kvadratnog korenovanja. (Znači možeš ih izvršiti konačno mnogo puta na elementima skupa je zatvoren za operacije sabiranja, oduzimanja, množenja, deljenja, kvadratnog korenovanja. (Znači možeš ih izvršiti konačno mnogo puta na elementima skupa 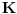 i kao rezultat dobiti opet element skupa i kao rezultat dobiti opet element skupa 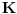 ) )E sad, ako bi našao opštu formulu koja je dobijena primenom konačno mnogo nabrojanih operacija, ona bi trebalo da važi za sve uglove, pa između ostalih i za one čiji je kosinus konstruktibilan a kosinus trećine nekonstruktibilan i tako bi došlo do kontradikcije. U ovom trenutku mogu samo da nagađam, da li se dotični trik može uopštiti tj. da li se može konstruisati neko nadpolje 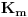 od od 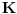 tako da obuhvati i sve brojeve oblika tako da obuhvati i sve brojeve oblika 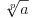 , , 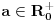 , za svako prosto , za svako prosto  za koji važi za koji važi 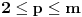 , a nakon toga "izvući iz šešira" neko zgodno , a nakon toga "izvući iz šešira" neko zgodno 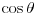 koje ne pripada datom skupu koje ne pripada datom skupu 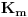 . . [ Farenhajt @ 28.12.2005. 09:25 ] @
Možda ja zaista jesam glup, ali opet ne vidim zašto se neprestano insistira na konstruktibilnosti broja kao kriterijumu za njegovu izrazivost u realnom domenu, gde dopuštam korene s bilo kakvim celobrojnim eksponentom.
Zaista ne vidim vezu između mogućnosti izvođenja određene konstrukcije samo lenjirom i šestarom (na šta se konačna kombinacija sabiranja, oduzimanja, množenja, deljenja i kvadratnog korenovanja svodi) i nemogućnosti da u određenim formulama "siđemo" iz kompleksnih brojeva u realne, tj. činjenice da očigledno realnu vrednost ne možemo izraziti bez kompleksnih brojeva. Recimo, u onoj mojoj kubnoj jednačini 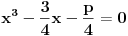 "tačka smutnje" jeste uslov "tačka smutnje" jeste uslov 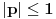 , dok za , dok za 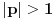 kao realnu nulu dobijaš vrlo čistu formulu kao realnu nulu dobijaš vrlo čistu formulu 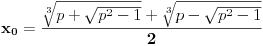 . .Čini mi se da se ti neprestano vrtiš oko konstrukcije pravilnog n-ugla, za koju (mislim) važi uslov da broj strana mora biti umnožak Fermaovih prostih brojeva 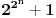 ... Ako grešim, unapred se izvinjavam. ... Ako grešim, unapred se izvinjavam.[ uranium @ 28.12.2005. 16:31 ] @
Ma ne, ne tvrdim ja da smo rešili tvoj problem, niti pokušavam da ga "gurnem pod tepih", naprosto ono što sam naveo o konstruktibilnim brojevima je samo jedna srećna okolnost koja nam omogućuje da odmah odbacimo jednu ogromnu klasu formula (a naravno ostaje neispitana još daleko veća klasa - upravo ona koja je tebi zanimljiva). Ja samo sugerišem da neko pokuša da uopšti tu ideju
[ Farenhajt @ 28.12.2005. 22:50 ] @
Pa onaj čika gore reče da to ima veze s Galoaovim teorijama... imamo li eksperta za tu temu u blizini?
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|