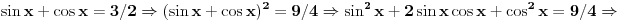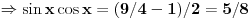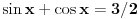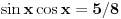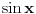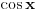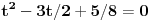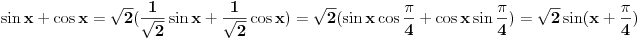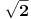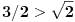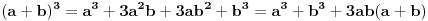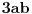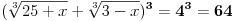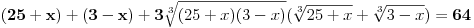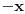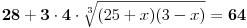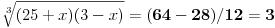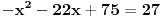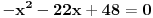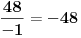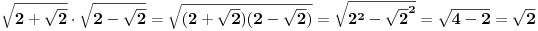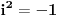[ Kretosh @ 28.12.2005. 13:39 ] @
| 1.jednacina sin x + cos x =3/2 na intervalu [0.2pi] ima koliko resenja? Pokusao sam da iskoristim: sin^2x+cos^2x=1 Pa sam zamenjivanjem jedne u drugu jednacinu dobio: 2cos^2x - 3 cosx=-5/4 Da sam dobio da je sa desne strane +5/4 bilo bi lako znao bih da jednacina nema resenja ali ovako ne znam sta dalje. 2. Proizvod resenja jednacine:  Probao sam da levu i desnu stranu dignem na kub ali time opet nisam uspeo da se resim korena. 3.Ako jer i imagionarna jedinica dokazati da je jedno od vrednosti izraza  odgovara izrazu odgovara izrazu  E kod ovog zadatka stvarno ne znam sta bih radio.Znam s je i^2=-1 i mozda bi se to moglo nekako iskoristii ali ja ne vidim kako bih stigao do resenja. U sustini ne trazim ispisana resenja zadataka vec ideje i objasnjenja ( mada ni resenja ne bi bila losha ;) |