Pretpostavljam da hoćeš da kažeš „skup pozitivnih realnih brojeva“ umesto „pozitivan realan broj“.

Odgovor na postavljeno pitanje je da. Dokazaću ovo na dva načina, od kojih prvi pokazuje eksplicitnu konstrukciju traženih podskupa a drugi je tu samo zanimljivosti radi, jer se rešenje dobija u jednom koraku pozivanjem na specijalan slučaj jedne vrlo lepe (ali i vrlo teške) teoreme.

1) Prvi način:

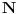
Najpre ćemo podeliti skup na traženi način. Neka su definisani sledeći skupovi:





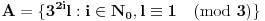
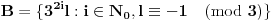
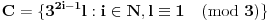
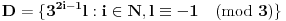
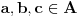
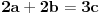
Dokazaćemo da ovi skupovi zadovoljavaju uslove zadatka. Pretpostavimo da postoje za koje važi . Imamo sledeće:

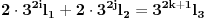
Neka je .
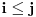
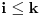
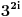
Ukoliko je deleći sve sa imamo:

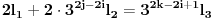
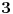
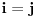
Pošto je desna strana deljiva sa , mora biti . Tada važi:

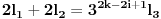
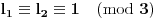
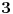
S druge strane, kako je sledi da leva strana nikad ne može biti deljiva sa . Kontradikcija.
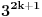
Još lakše, ukoliko je , deleći sve sa imamo:

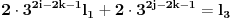
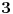
pa je leva strana deljiva sa a desna nije.

Analogno se pokazuje da data jednačina nije rešiva ni u ostalim podskupima.

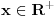
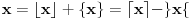
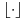
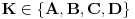
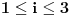
Za koristićemo oznake , gde su sa i standardno označeni donji i gornji ceo deo, redom. Za i označimo:



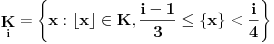
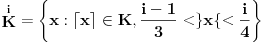
Potrebna su nam još dva skupa, naime:



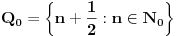
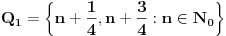
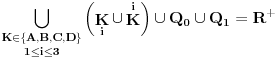
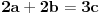
Lako se proverava da su svi ovi skupovi međusobno disjunktni i da je . Preostaje još da se dokaže da jednačina nije rešiva ni u jednom od njih.

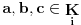
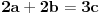
Neka i pretpostavimo da važi . Tada:


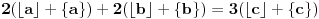
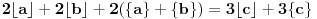
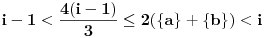
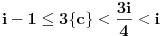
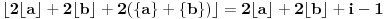
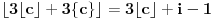
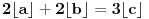
Iz ograničenja sledi i , odakle zaključujemo da mora važiti i pa je što je nemoguće na osnovu već dokazanog jer .

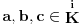
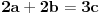
Slično, ako i onda imamo:



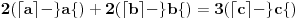
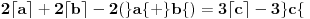
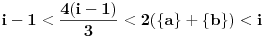
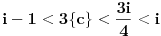
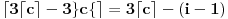
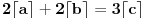
Pošto je i sledi i , odnosno što je nemoguće, slično malopređašnjem objašnjenju.

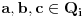
I poslednje, ako onda je leva strana jednakosti ceo broj a desna nije, pa jednačina nema rešenja ni u ovom skupu.

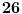
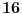
Za kraj samo da napomenem da, kao što se može prebrojati, ovo rešenje uključuje podskupa. Ovo nikako nije minimum, štaviše relativno jednostavnom modifikacijom ovo rešenje možemo svesti na podskupa, ali sam se odlučio za ovo jer je prirodnije a broj podskupa ne igra veliku ulogu.

2) Drugi način:

Definicija 1:

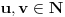
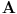
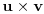
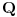
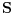
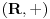
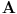
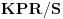
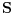
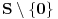
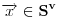
Neka i neka je matrica sa elementima iz . Neka je potpolugrupa od . Tada kažemo da za važi (kernel partition regular over ) akko kad god je obojen sa konačno mnogo boja postoji monohromatski takav da je .

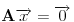
Definicija 2:

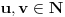
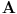
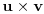
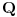
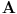
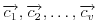
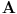
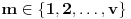
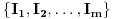
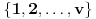
Neka i neka je matrica sa elementima iz . Označimo kolone od sa . Tada zadovoljana uslov kolona akko postoji i particija skupa u neprazne podskupe takva da važi:
a) ;
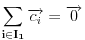
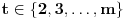
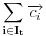
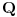
b) za svako , je linearna kombinacija sa koeficijentima iz vektora iz .

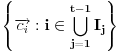
Teorema: (Rado)

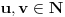
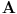
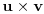
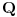
Neka i neka je matrica sa elementima iz . Sledeći iskazi su ekvivalentni:
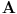
a) je ;
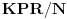
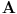
b) je ;
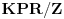
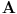
c) je ;
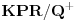
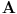
d) je ;
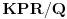
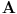
e) je ;
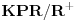
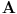
f) je ;
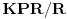
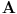
g) zadovoljava uslov kolona.

Primenom ove teoreme rešenje zadatka dobijamo u jednom koraku. Zaista, neka je

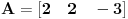
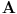
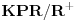
Nemoguće je zadovoljiti uslov a) iz Definicije 2, pa sledi da ne zadovoljava uslov kolona, pa iz Teoreme dobijamo da nije , što je ekvivalentno pitanju iz zadatka.

Da vidimo još neke zanimljive posledice Radove teoreme.

Šurova teorema:

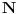
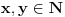
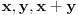
Za svako bojenje skupa u konačno mnogo boja postoje takvi da su iste boje.

Dokaz:

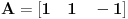
Primenimo Radovu teoremu na matricu koja zadovoljava uslov kolona.

Van der Waerden's Theorem:

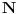
Za svako bojenje skupa u konačno mnogo boja postoji konačna monohromatska aritmetička progresija proizvoljno velike dužine.

Dokaz:

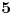
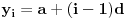
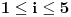
Pretpostavimo da želimo da pokažemo da postoji aritmetička progresija dužine (slično ide za bilo koju dužinu). Neka je za . Tada od sistema jednačina:



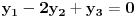
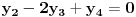
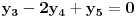
pravimo sledeću matricu:

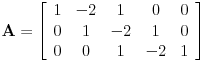
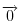
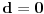
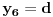
Zbir svih kolona ove matrice je pa ona zadovoljava uslov kolona. Ipak, život nam nije tako lep pošto sve što nam Radova teorema garantuje u ovom slučaju je da postoji aritmetička progresija makar sa , što nije ono što nas zanima. Ovo se da lako popraviti, naime možemo staviti i tražiti da i ono bude iste boje iz jednačine

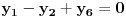
Tada je

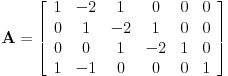
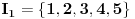
koja zadovoljava uslov kolona kad uzmemo i .

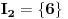
Literatura:

[1] R. Rado, Studien zur Kombinatorik, Math. Zeit. 36 (1933), 242-280.
[2] R. Rado, Note on combinatorial analysis, Proc. London Math. Soc. 48 (1943), 122-160.

_{[Ovu poruku je menjao Bojan Basic dana 19.04.2006. u 02:09 GMT+1]}