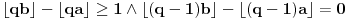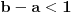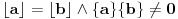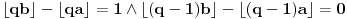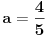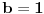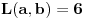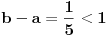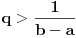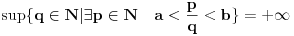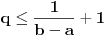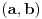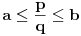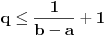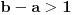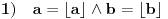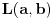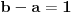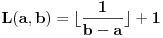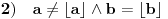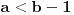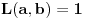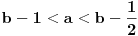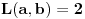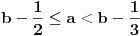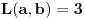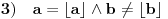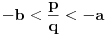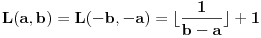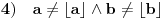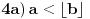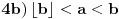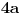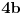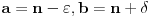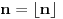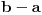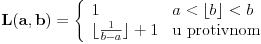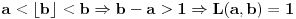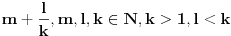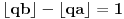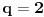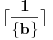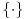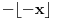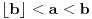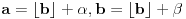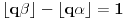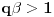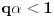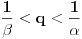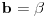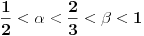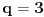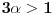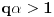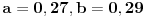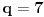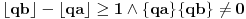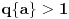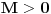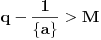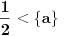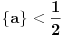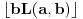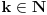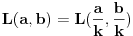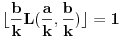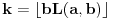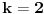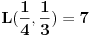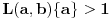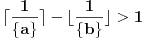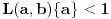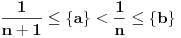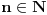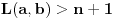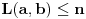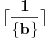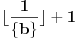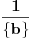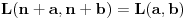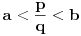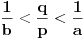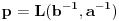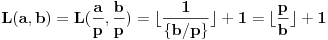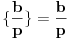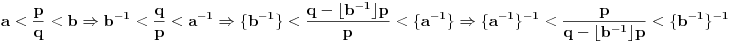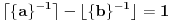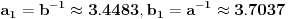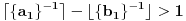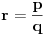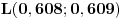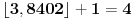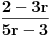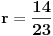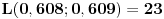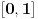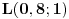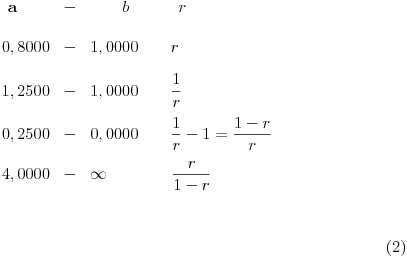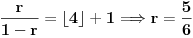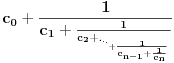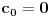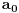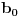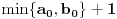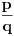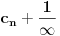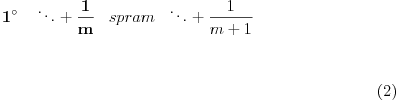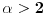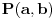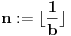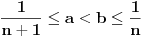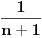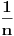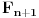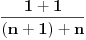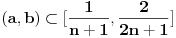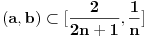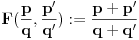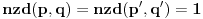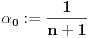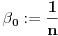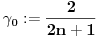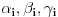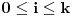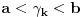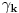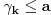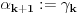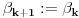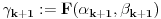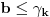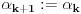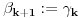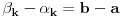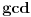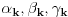|
|
[ Farenhajt @ 04.01.2006. 01:33 ] @
Hm, ako sam te dobro shvatio, zaključujem da bi traženo  trebalo da bude rešenje sistema 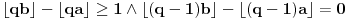 - ali ne znam je li to od pomoći niti kako bi se ti uslovi u najopštijem slučaju rešili. Naravno, očigledno je da je 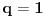 za 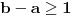 i 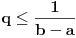 za 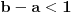 . Ali, udubiću se kasnije 
Napomena: Ako 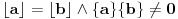 , onda se sistem sastoji od dve jednačine: 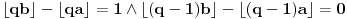 .
[Ovu poruku je menjao Farenhajt dana 04.01.2006. u 03:05 GMT+1][ uranium @ 04.01.2006. 05:38 ] @
Sviđa mi se u kom pravcu razmišljaš  (veliko hvala na zanimljivim idejama) i dakle, slažem se sa svime što si napisao, osim što mi ovo nije jasno: Citat: Farenhajt: 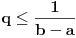 za 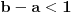 .
Jer na primer: 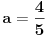 i 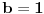 daju 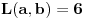 i 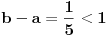 pa dobijamo 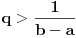 .
Inače, nisam pomenuo, jer mi se činilo da nije bitno ali 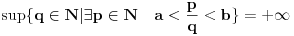 [ srki @ 04.01.2006. 08:35 ] @
Citat: Farenhajt: 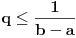 za 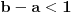 .
Mala ispravka, treba 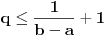 [ Farenhajt @ 04.01.2006. 08:46 ] @
Kontraprimer stoji. Dakle, pošto se dati uslov svodi na 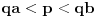 , ideja je da posmatramo niz intervala 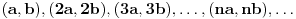 , sa zaključkom da je "rastezanje" intervala 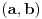 dovoljno dovoljno vršiti dok ne postane dugačak bar 1, jer će onda zasigurno obuhvatiti i neki ceo broj (što naravno ne znači da se do celog broja ne može stići i u manje rastezanja - cf. kurziv). Na osnovu ove ideje s "rastezanjem" se i očigledno formulišu oni uslovi s celim delovima.
Biće da sam podsvesno radio sa 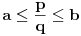 , u kom slučaju tvoj primer ima trivijalno rešenje 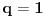 .
Međutim, možda mogu da se iščupam s procenom 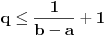 , jer će onda interval postati strogo duži od  , pa će važiti i stroge nejednakosti.
Naravno, ovaj supremum koji si naveo stoji (očit je i iz procedure "rastezanja"), ali nam on neće pomoći da nađemo minimalno  .
EDIT: Srki me preduhitrio sa zaključkom  I kad već ispravljamo, onda treba izbaciti " 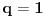 za 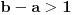 " jer se to automatski dobija iz 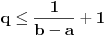 .
DODATAK: Treba doterati i uslove s celim delovima, jer ako su  i  uzastopni celi brojevi, kao rešenje se dobija  , a treba nam  .
[Ovu poruku je menjao Farenhajt dana 04.01.2006. u 10:32 GMT+1][ Farenhajt @ 04.01.2006. 11:50 ] @
Elem, malo sam se pozabavio, te ću vas sad smarati s razdvajanjem slučajeva:
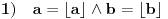
Ovde 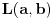 mora biti  za 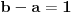 i  za 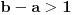 . Oba slučaja objedinjuju se formulom 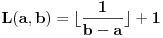 ;
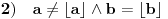
Ako je 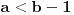 , onda je 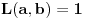 ; ako je 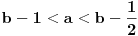 , onda je 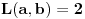 ; ako je 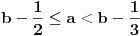 , onda je 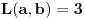 ; i tako dalje. Formula će glasiti 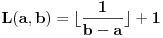 ;
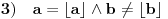
Ovaj slučaj možemo svesti na prethodni ako posmatramo 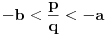 , pa zaključujemo da je 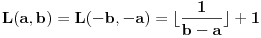 ;
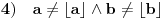
Ovde moramo razlikovati dve mogućnosti:
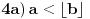 . Tada je 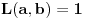
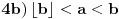 . Tada je 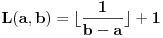
(Ne vidim kako bi se 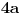 i 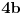 objedinili u jednu formulu, ali su ideje dobrodošle. Slučaj 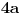 pokriva situacije tipa 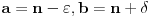 gde je 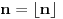 , a  i  proizvoljno mali pozitivni brojevi - tu nam baratanje s 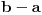 ničemu ne služi.)
Dakle, kad sve sumiramo, dobijamo 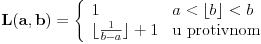 .
(Napomena: Slučaj  obuhvaćen je prvom granom funkcije jer ako je  celobrojno, onda 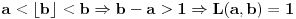 )
Izvol'te s diskusijom i kontraprimerima.
[Ovu poruku je menjao Farenhajt dana 04.01.2006. u 13:12 GMT+1][ srki @ 04.01.2006. 12:24 ] @
Da budem iskren nisam bas citao tvoju poruku nego sam letimicno preleteo. Da li je ovaj primer obihvacen tvojom formulom:
npr. a=4.499999999999999999999 b=4.50000000000000000000000000001.
Tu bi resenje bilo q=2 a p=9.
[ Farenhajt @ 04.01.2006. 12:42 ] @
U pravu si, formula ne radi za taj slučaj, kao ni za srodne slučajeve "okolina" brojeva 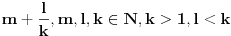 , što bi potpadalo pod slučaj 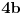 .
Ali nek to uranium krpi 
Elem, tu se vraćamo na onu prvu ideju, da se traži minimalno rešenje jednačine 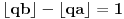 . Ta jednačina za tvoj primer daje ispravno rešenje 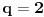 .
[Ovu poruku je menjao Farenhajt dana 04.01.2006. u 13:49 GMT+1][ Farenhajt @ 04.01.2006. 13:27 ] @
Evo dokonah nešto: Mislim da se taj slučaj može rešiti preko izraza 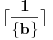 , gde je  "ceiling" funkcija (ne znam joj ime na srpskom), dakle najmanji ceo broj ne manji od argumenta funkcije, a 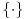 je razlomljeni deo. (Inače se "ceiling" može izraziti kao 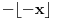 ).
Dakle, ako u slučaju 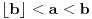 stavimo 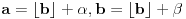 , onda se jednačina iz prethodne poruke svodi na 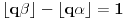 . Ovo pak znači da je 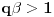 i 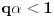 , odakle dobijamo 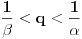 . Na osnovu ovoga zaključujemo da je najmanje takvo  dato izrazom iz prvog pasusa.
Dopune?
[Ovu poruku je menjao Farenhajt dana 04.01.2006. u 14:28 GMT+1][ uranium @ 04.01.2006. 19:46 ] @
Neka je  , 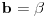 i 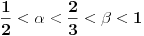 , onda imamo da je traženo 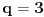 , ali 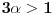 .
Znači ipak imamo dva podslučaja, onaj koji je rešio Farenhajt i ovaj drugi kada je 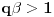 i 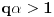 iz koga sledi 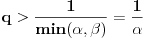 .
[ Farenhajt @ 04.01.2006. 21:46 ] @
Da, ja sam se ograničio na slučaj kad 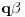 premaši  , a 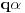 ostane manje od  . Naravno, u opštem slučaju će prvi izraz premašiti neko  , a drugi će ostati manji od  .
Što se primera tiče, recimo za 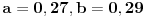 treba dobiti 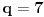 , a to ne proizlazi ni iz jedne dosad ponuđene formule, osim iz numeričkog rešavanja sistema 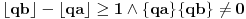 .
[Ovu poruku je menjao Farenhajt dana 04.01.2006. u 22:52 GMT+1][ uranium @ 05.01.2006. 05:51 ] @
Ovo što sledi odnosi se samo na preostali podslučaj slučaja 4b.
Primetimo to da ako 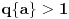 , donja granica koju dobijamo za broj  izgleda neupotrebljiva jer se za svako unapred dato 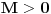 mogu naći  i  tako da bude 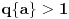 i 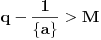 . Pomenuo bih još samo to da je ovakvih slučajeva neprebrojivo mnogo (svako  za koje je 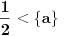 ali i još neprebrojivo mnogo onih za koje je 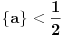 ) [ Farenhajt @ 05.01.2006. 06:58 ] @
Ideja (koju pišem kako mi je pala na pamet, te nemam pojma je li plodonosna): Ispostavilo se da su nam problematični samo oni slučajevi gde je 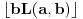 (ili 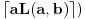 , to jest ono  iz inicijalne postavke) veće od 1.
Možemo li sačiniti algoritam u suprotnom smeru - dakle, možemo li sažeti interval 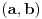 tako da 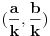 dospe u okolinu broja čiji je razlomljeni deo oblika 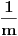 ? [ uranium @ 05.01.2006. 20:30 ] @
Ako sam dobro razumeo, tražimo 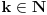 tako da 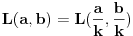 i da pri tom bude 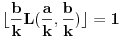 . Ideja je odlična, ali jedini problem je u tome što moramo uzeti da bude baš 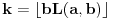  Znači pitanje je da li se može doći do neke dobre procene za  a da to ne zahteva previše dobru procenu za 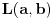 .
Primer: 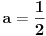 , 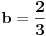 , onda je 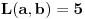 i 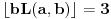 , pa ako bi probali sa 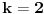 , dobili bi da je 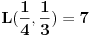 i 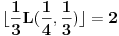 , pa smo opet došli na problematičan slučaj. Takođe, ne vidim neki način (osim direktne provere) da utvrdimo da li je slučaj (kada je 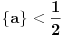 ) problematičan ili ne.
U svakom slučaju, od srca se zahvaljujem na svoj dosadašnjoj pomoći, pre svih Farenhajt-u a naravno i srki-ju.  [ uranium @ 06.01.2006. 05:31 ] @
Ipak sam našao način da odredimo da li se radi o problematičnom podslučaju ili ne:
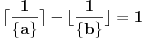 akko je podslučaj problematičan tj. 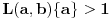
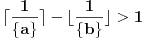 akko podslučaj nije problematičan tj. 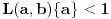 .
Za obrazloženje je dovoljno da primetimo da uvek važi tačno jedna od sledeće dve situacije:
1. 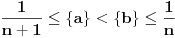 2.
2. 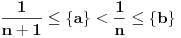
za pogodno izabrano 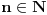 .
U prvom slučaju je 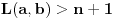 , pa dobijamo 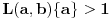 a u drugom slučaju je 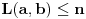 pa je 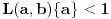 .
[ Farenhajt @ 07.01.2006. 01:36 ] @
Evo tri bitna rezultata koja su nam dosad promakla:
Pre svega:
Citat: Farenhajt
Evo dokonah nešto: Mislim da se taj slučaj može rešiti preko izraza 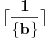
1. Tačan izraz treba da glasi 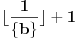 , jer će se za celobrojno 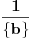 u prvom slučaju dobiti pogrešan rezultat.
2. Ako je 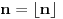 , jasno je da je 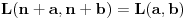 . Dakle, sva razmatranja slučaja 4b možemo svesti na interval  , te ćemo nadalje podrazumevati da je 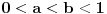 .
3. Iz 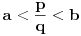 sledi 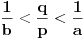 , te zapravo možemo staviti 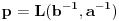 . Ukoliko ovaj slučaj nije problematičan, tj. ako potpada pod 1,2,3,4a, našli smo  , te onda imamo da je 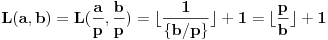 , pošto je 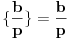 . Ukoliko slučaj jeste problematičan, dakle ako opet potpada pod 4b, ponavljamo postupak svodeći brojeve na razlomljene delove, imajući u vidu da važi sledeće: 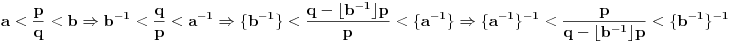 . Iz ovoga sledi da ćemo konačnim brojem rekurzija sigurno stići do imenioca  , te ćemo onda lako dobiti i  i  .
E sad, da li ovo ikako koristi... uraniume, priskoči i razradi 
Numerički primer:
1. 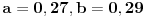 . Slučaj je problematičan jer je 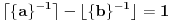 .
2. 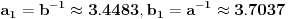 . Ovaj slučaj nije problematičan jer 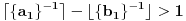 . Stoga dobijamo 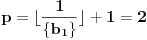 .
3. Polazni interval sažimamo na 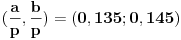 i sada je 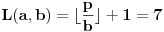 [Ovu poruku je menjao Farenhajt dana 07.01.2006. u 11:49 GMT+1]
[Ovu poruku je menjao Farenhajt dana 07.01.2006. u 11:49 GMT+1][ Farenhajt @ 07.01.2006. 11:28 ] @
Dodatak
Na osnovu iznetog u prethodnoj poruci, može se formulisati opšti numerički postupak za traženje razlomka 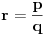 . Najlakše će biti da se postupak ilustruje primerom. (Napomena: U tabeli se parne vrste dobijaju od neparnih uzimanjem recipročnih vrednosti svih argumenata, a neparne od parnih svođenjem argumenata na interval  . Takođe, u koloni a nalaze se transformacije argumenta  , a u koloni b transformacije argumenta  , što znači da u nekim vrstama veći broj dolazi pre manjeg. To, međutim, nije od značaja za postupak. Sve vrednosti zaokruživane su na 4 decimalna mesta.)
Naći 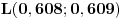

Na kraju stižemo do intervala unutar koga se nalazi ceo broj i tu obustavljamo postupak. Uzimamo vrednost 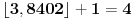 i izjednačavamo je sa 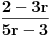 . Rešavanjem jednačine dobijamo 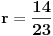 . Dakle, 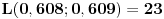 .
Postupak, koliko mi se čini, funkcioniše i na segmentu 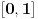 :
Naći 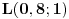
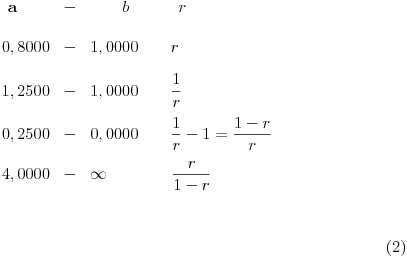
Sada imamo 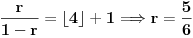 .
[Ovu poruku je menjao Farenhajt dana 07.01.2006. u 15:53 GMT+1]
[ uranium @ 07.01.2006. 15:35 ] @
Farenhajte, svaka ti čast za ovo što si smislio!!! 
Nemam reči (nor appropriate emoticons  ) kojima bih iskazao divljenje...
Veliko ti hvala! 
[ Farenhajt @ 07.01.2006. 16:08 ] @
Dodatak 2
U stvari, kad se bolje proanalizira, zaključujemo sledeće:
Brojeve  i  treba razviti u verižne razlomke po modelu 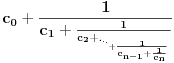 (gde je 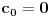 za brojeve iz intervala  , ali u opštem slučaju nema prepreke da bude i veće od nule). Zatim se odgovarajuće karike u ta dva razvoja porede. Čim se pronađu karike koje se razlikuju za barem  (obeležimo te karike sa 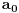 i 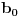 ), razlomak se tu preseca i završava vrednošću 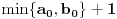 , pa se onda tako dobijeni verižni razlomak vraća u svedenu formu, čime se dobija traženi razlomak 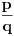 .
Ukoliko razvoji imaju različit broj karika, treba zamisliti da se kraći završava sa 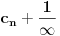 .
Ukoliko je 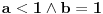 (ili uopšteno 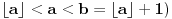 , onda se u razvoju broja  gledaju samo prva i druga karika: ukoliko je prva karika veća od 1, odbacuje se čitav razvoj posle te karike, a vrednost karike ostaje nepromenjena, a ukoliko je prva karika jednaka 1, razvoj se prekida posle druge karike i ta se karika povećava za jedan.
Očigledno, ovako formulisan postupak može funkcionisati i za 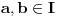 , s tim što će se karike i generisati i porediti jedna po jedna.
[Ovu poruku je menjao Farenhajt dana 08.01.2006. u 17:26 GMT+1]
[ Bojan Basic @ 07.01.2006. 20:37 ] @
Evo i drugog algoritma: krenemo redom od jedinice i čekamo kad ćemo dobiti ceo broj u intervalu koji se dobija kada pomnožimo početni interval sa brojem koji imamo.
E sad, mene zanima koja je razlika između ovog i Farenhajtovog algoritma? Iz navedenih primera mi deluje da je njegov algoritam brži, ali da li je zaista tako ili ima neka druga caka?
Izvinjavam se što nisam mnogo razmišljao o ovome što sam napisao, pa ako sam lupio nešto očigledno nemojte zameriti.
[ Farenhajt @ 08.01.2006. 12:31 ] @
Dodatak 3
Na sugestije cenjenog uraniuma, formulišem nekoliko specijalnih slučajeva u kojima treba modifikovati kriterijume upoređivanja verižnih razlomaka, budući da inicijalni zadatak zahteva stroge nejednakosti. Svi slučajevi opisuju završne karike verižnih razvoja i podrazumeva se da pre njih nisu nađene nejednake karike.
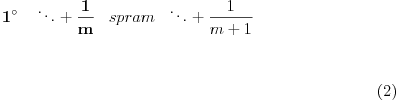
Ovde se oba razvoja proširuju kao 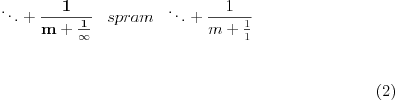
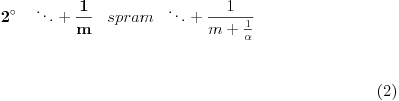 , gde je  ceo broj ili verižni razlomak
Slično kao gore, prvi razvoj se proširuje pa imamo 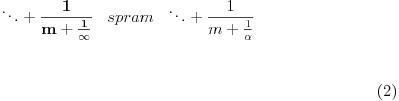
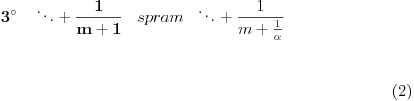 , gde je  ceo broj ili verižni razlomak
Prvi razvoj se proširuje, pa imamo 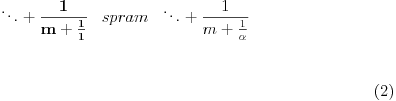 . Ako je  ceo broj, ovo se za 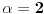 svodi na 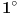 , a za 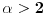 ne postavlja problem. Ukoliko je  verižni razlomak, prvi razvoj može biti neophodno dodatno proširiti kao 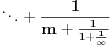 ukoliko prvobitnim proširenjem dobijamo neki od već obrađenih slučajeva.
@Bojan
Od algoritma koji pominješ upravo smo i pošli:
Citat: Farenhajt:
...zaključujem da bi traženo  trebalo da bude rešenje sistema 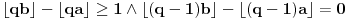
(Naravno, uz neophodne modifikacije zbog zahtevanih strogih nejednakosti.) Međutim, od onda se stvar razvila.
[Ovu poruku je menjao Farenhajt dana 08.01.2006. u 13:33 GMT+1]
[ Bojan Basic @ 08.01.2006. 15:05 ] @
Pratio sam temu od početka, nikad ne volim da upadam kao s Marsa. Ono što sam pokušao da pitam u prošloj poruci (verovatno se nisam najbolje izrazio), je na osnovu čega znamo da je taj razvijeni algoritam efikasniji od onog trivijalnog i da li bi se možda mogao konstruisati primer gde trivijalni algoritam brže stiže do rešenja od razvijenog?
[ Farenhajt @ 08.01.2006. 16:10 ] @
Zavisi i šta podrazumevaš pod brzinom. U trivijalnom algoritmu u svakom koraku imaš dve operacije sabiranja i dve operacije poređenja - "dodaj jedno  levo i jedno  desno, pa vidi da li je leva strana strogo manja od celog dela desne strane i desna strana strogo veća od svog celog dela" - ali zato brojčano više koraka (čini mi se), dok u izvedenom algoritmu imaš manje koraka ali više računskih radnji. Sa stanovišta procesorskog vremena, nisam siguran koji je brži.
Međutim, izvedeni je doveo do rezultata s verižnim razlomcima, a taj mi se čini teorijski bitan i verovatno bi se moglo dokazati da je zapravo i najbrži.
[Ovu poruku je menjao Farenhajt dana 08.01.2006. u 17:12 GMT+1][ uranium @ 08.01.2006. 19:22 ] @
Evo da opišem i ja jedan algoritam (koji je verovatno sporiji od svih navedenih).
Neka je 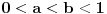 .
Neka nam predikat 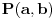 označava da li je slučaj problematičan ili ne, tj. 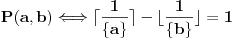 .
Evo ukratko u čemu je ideja - pa ću onda to i formalizovati.
Ako nije 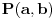 , stvar je gotova - upotrebimo Farenhajtovu formulu.
Ako jeste 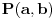 , onda uzmimo da je 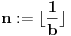 , pa mora da važi: 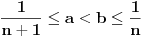 . Brojevi, 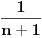 i 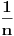 su susedni članovi Farey-evog niza 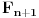 . Sada generišemo jedan međučlan 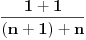 ako je on upao u interval 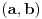 našli smo broj koji smo tražili, a ako nije postupak nastavljamo sa međučlanom i jednim od prethodnih (zavisno od toga da li je 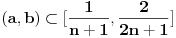 ili je 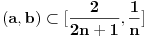 . Jasno je da se algoritam kad tad zaustavlja.
Evo sad isto to samo dosadnije 
Radi lakšeg izražavanja posmatrajmo i funkciju 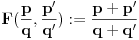 , pri čemu je 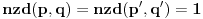 .
Neka je 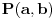 . Stavimo da je 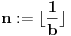 , 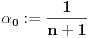 i 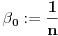 , 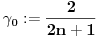 . Pretpostavimo da su već definisani svi brojevi 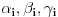 za 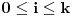 onda:
1. Ako je 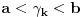 tu stajemo - jer je 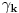 upravo ono što smo tražili.
2. Ako je 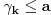 , onda stavimo da je 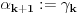 i 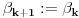 , 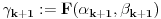 .
3. Ako je 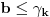 , onda stavimo da je 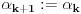 i 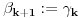 , 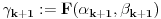 .
Jasno je da će postupak u najgorem slučaju trajati dok se ne desi da 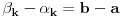
Ključna stvar je u tome da za susedne članove Farey-evog niza, pomoću f-je  uvek dobijamo novi (njima susedni) član koji se nalazi između njih a ima najmanji mogući imenilac.
[Ovu poruku je menjao uranium dana 08.01.2006. u 21:06 GMT+1][ Farenhajt @ 09.01.2006. 03:24 ] @
Ne deluje sporiji od onog s reciprociranjem, bar na prvi pogled. A računski je daleko jednostavniji  [ uranium @ 09.01.2006. 11:04 ] @
Samo na prvi pogled izgleda jednostavniji - jer ona f-ja  u stvari krije u sebi f-ju 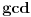 (verovatno sam loše objasnio, ali sam mislio da se njen output uvek dovede u sveden oblik - a za to bih potrošio jedno 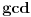 i dva deljenja), a zavisno od načina predstavljanja brojeva 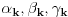 ni ono nalaženje brojioca i imenioca ne mora biti zanemarljivo 
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|
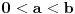 pronaći najmanje
pronaći najmanje 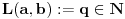 tako da
tako da 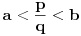 za neko
za neko 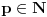 .
. i
i  . Takođe, dobrodošle su i sve ideje u vezi sa specijalnim slučajem
. Takođe, dobrodošle su i sve ideje u vezi sa specijalnim slučajem 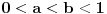 ili
ili 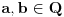 .
.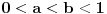 .
. 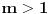 i uočimo sve razlomke
i uočimo sve razlomke 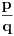 gde je
gde je 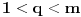 i
i 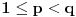 . Sada uočimo skup svih otvorenih intervala (sadržanih u
. Sada uočimo skup svih otvorenih intervala (sadržanih u  ) u kojima nema ni jednog od uočenih racionalnih brojeva. Na kraju, od tih intervala napravimo skup
) u kojima nema ni jednog od uočenih racionalnih brojeva. Na kraju, od tih intervala napravimo skup  samo onih intervala koji sadrže i barem jedan razlomak oblika
samo onih intervala koji sadrže i barem jedan razlomak oblika 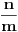 (
(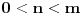 ). Dakle, za svako
). Dakle, za svako 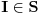 važi
važi 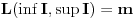 . Primetimo i to je
. Primetimo i to je 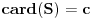 .
.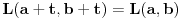 , ali nisam previše "kopao" u tom pravcu...
, ali nisam previše "kopao" u tom pravcu...