Tacan je i jedan i drugi rezultat. Zavisi kako je u zadatku definisan ugao .
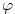
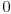
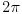
Ako je definisano da ide od do onda je rezultat
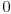
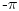
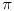
a ako je definisano da ide od do onda je rezultat .

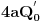
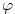
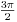
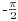
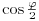
Sada cu da ti objasnim ako ti nije jasno zasto se to razlikuje. Ti verovatno mislis da je svejedno da li uzmes da je recimo ili . E pa nije jer ce biti razlicit u jednom i u drugom slucaju.

Prvi put pisem nesto u tex-u. U cemu gresim? Zasto nece da mi napise kako treba 3Pi/2 ? Napisao sam \frac {3\pi}{2}. Evo sada kada sam dodao ispred i iza $ onda radi.
Cemu sluzi $?


[Ovu poruku je menjao srki dana 22.10.2002. u 10:55 GMT]

Naravno, matematički mi je potpuno jasno, mora u postavci biti definisan taj ugao, to je potpuno jasno kažem. Mene više zanima ona realna (fizička) strana. To onda znači da ta kontura u stvarnosti ima razlicite količine naelektrisanja ? To je ono što me buni ...

Što se tiče texa, sa $ naznačavaš texu da počinješ da pišeš matematiku (posle završene math. formule opet staviš $), a može i ovako:

\begin {displaymath}

formule, formule, ... (sad bez $)

\end {displaymath}

Takođe, možeš primetiti kako većina formula koje si napisao "lebdi", to je izgleda neki bag, jer ako ti pređe linija texa, koju pišeš, u sledeći red, onda, čini mi se, to bude ovako ružno formatirano. Gojko ?

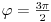
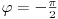
Kontura zaista ima razlicitu raspodelu naelektrisanja u zavisnosti od toga kako je ugao definisan. Dao sam ti primer da je razlicito naelektrisanje za i za iako je to ista tacka na konturi.

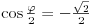
U prvom slucaju je a u drugom je .

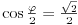
Znaci u jednom slucaju na istoj tacki dobjemo negativno a u drugom slucaju pozitivno naelektrisanje.

Znaci u zadatku mora obavezno biti definisan ugao da bi naelektrisanje bilo jednoznacno raspodeljeno.

[Ovu poruku je menjao srki dana 25.10.2002. u 12:09 GMT]

[Ovu poruku je menjao srki dana 25.10.2002. u 12:48 GMT]

Zadatak nije trivijalan.

Obrati pažnju kako je definisan ugao! U slučaju da je ugao
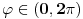
, gustina linijskog naelektrisanja nije neprekidna funkcija u tački što za posledicu ima pojavu tačkastog naelektrisanja u tački pored postojećeg linijskog usled singulariteta gradijenta linijskog naelektrisanja! Granični uslovi u Maksvelovim jednačinama i sračunaj.

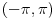
Ako je ugao definisan na intervalu na granicama intervala naelektrisanje je pa je sve OK.

f

Strogo govoreći, to nije tačno. Dokle god su granični uslovi zadovoljeni, svaka raspodela naelektrisanja je moguća.

To što je s jedne strane neke tačke linijska gustina naelektrisanja jedna a s druge druga, znači da se u toj tački pojavljuje dodatno tačkasto naelektrisanje, (osim linijskog koje je pomenuto u zadatku) koje je posledica zadovoljenja graničnih uslova. To se ne sme izgubiti iz vida.

f

Ma da, ali sam mislio konkretno u ovom slucaju da se dobija razlicita raspodela naelektrisanja.