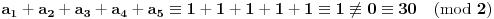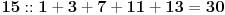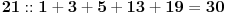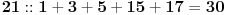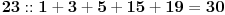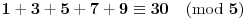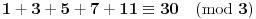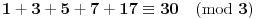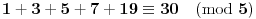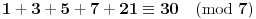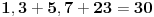[ Night_RaptOr @ 07.01.2006. 19:10 ] @
|
| Imas neparne brojeve : 1,3,5,7,9,11,13,15,17,19,21,23,25,27,29.
Moras naci 5 neparnih brojeva koji kad se saberu daju broj 30, a ne smijes koristiti 2 puta iste brojeve.
resenje postoji !!! samo ima jedna caka |
[ uranium @ 07.01.2006. 20:34 ] @
Baš da vidimo u čemu je caka

jer u protivnom:
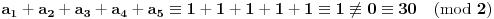
vidimo da zadatak nema rešenja

(uslov o neponavljanju sabiraka je suvišan?)
[ Farenhajt @ 07.01.2006. 21:20 ] @
Pa, recimo, u sistemu s osnovom 25 važiće 5+7+9+11+13=30
[ uranium @ 07.01.2006. 22:44 ] @
[ kurt.hectic @ 08.01.2006. 01:26 ] @
Citat:
Pa, recimo, u sistemu s osnovom 25 važiće 5+7+9+11+13=30
U sistemu sa osnovom 25 brojevi (1,1) i (1,3) su parni jer je (1,1) = (13) + (13), a (1,3) = (14) + (14). Traži se brojevi budu neparni.
[ uranium @ 08.01.2006. 03:44 ] @
@kurt.hectic:
Dakle, na osnovu tvoje primedbe možemo da zaključimo da se zaista ne radi o (ili ne samo o) interpretaciji datih zapisa u nekoj drugoj osnovi, jer ako je osnova neparna, onda nisu svi polazni brojevi neparni. A ako je osnova parna, onda opet imamo kontradikciju, jer zbir neparno mnogo neparnih brojeva ne može dati paran rezultat.
[ Farenhajt @ 08.01.2006. 09:21 ] @
A moguća je i ovakva caka:
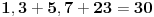
[ chupcko @ 09.01.2006. 09:41 ] @
A na kraju ce biti caka kao sa akrobatama, tako ce 9 da postane 6 :).
E sada, kako sam krenuo da pronalazim punoooooo raznih kombinacija, bolje da stanem :).
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.