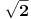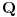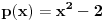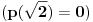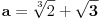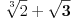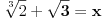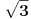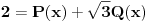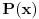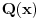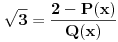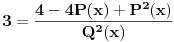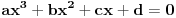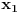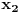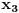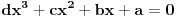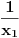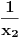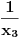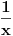Prvo, prosto receno, broj x je algebarski nad nekim poljem E ako postoji polinom sa koeficijentima iz tog polja,
takav da mu je x koren.

Npr:
realan broj jeste algebarski nad poljem racionalnih brojeva
jer postoji polinom kome je to koren


Realan broj nije algebarski nad jer ne postoji polinom sa racionalnim koeficijentima kome je koren

Skup svih algebarskih brojeva je polje, a u polju svi elementi (osim 0) imaju inverz u odnosu na mnozenje.
Dakle, ako je x algebarski (nad nekim poljem) onda je i 1/x algebarski.

Sto se tice broja
treba ti polinom, nadjes ga tako sto se oslobodis ovih korena, to jest dignes ovo na sesti stepen,
sredis malo i eto ga.

Jednostavnije od ovoga ne moze, nadam se da ti je bar jasnije.

a jooooooooooooooj opet ne kontam!! ja mislim da ne mogu samo napisat da je skup svih algebarskih brojeva polje, a da u polju svi elementi (osim 0) imaju inverz u odnosu na mnozenje, nego da tribam dokazat da svi elementi (osim 0) imaju inverz u odnosu na mnozenje!! biće sam bubla neku glupost al stvarno ništa ne kontam ta polja i ostalo! pliiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiz probaj još jednostavnije objasnit!!!!
p.s. kad bi ono sve stavila na 6u, polinom bi bio sigurno smiješno izgledo x^6-neki brojevi, jes da bi to bio jedan broj da se izračuna na digitron, al glupo je!! zašto bi zadali zadatak da provjere znamo li množenje??
mislim jel se može nekako dokazat da je zbroj dva alg br isto alg.br????

Ukratko, neki broj se zove algebarski ako možeš pronaći polinom čiji je taj broj koren, tj. za koji je vrednost polinoma nula.

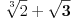
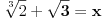
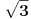
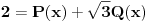
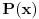
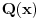
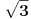
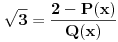
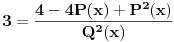
Dakle, treba da nađeš polinom čija je nula . Stavi , onda prebaci na drugu stranu i sve digni na kub. Dobićeš izraz , gde su i neki polinomi. Sad iz toga izrazi : , pa to kvadriraj: . Sad se reši razlomka, isprebacuj sve na jednu stranu, sredi i dobićeš jednačinu čije je rešenje polazni broj.

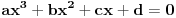
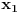
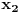
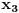
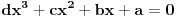
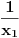
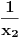
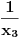
A što se drugog pitanja tiče, u algebri se dokazuje da ako koeficijente nekog polinoma uzmeš obratnim redom (dakle, koeficijent uz član s najvišim stepenom staviš kao slobodni i tako redom), onda njegove nule postaju recipročne vrednosti nula originalnog polinoma. 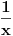(Primer: Ako kubna jednačina ima rešenja , i , onda jednačina ima rešenja , i .) Dakle, ako broj jeste nula nekog polinoma, onda se može naći polinom čija je nula , pa je i taj broj algebarski.

_{[Ovu poruku je menjao Farenhajt dana 10.01.2006. u 06:23 GMT+1]}

hvala!!!!!!!!!!!! sad mislim da sam skontala!!