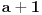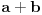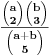[ Elojd @ 19.01.2006. 14:08 ] @
|
| Zadatak glasi:
Citat: U kutiji ima a belih i b crnih kuglica (a>=2, b>=3).Odjedanput se izvlači pet kuglica. Naći verovatnoću da su izvučene dve bele i tri crne kuglice
Mene zanima, pošto je verovatnoća P=m/n (m-broj povoljnih rez., n-ukupan broj rezultata), kako to da je u rešenju dato da je n=
(a+b)
( 5 )
^^ ovo je binomni obrazac
tj. kombinacije 5 klase od a+b elemenata BEZ ponavljanja. Mene buni kako to da nisu u pitanju kombinacije sa ponavljanjem, jer ipak se ponavljaju boje .Npr mozemo dobiti bbccc ili bbbcc. Izgleda da se izvucene kulice posmatraju kao posebni elementi, odnosno da prva bela nije isto sto i druga bela. To mi nije jasno? Znači da se slučaj bbbbb ne sastoji od istih elemenata iako su u pitanju identične boje. Da li neko može ovo da mi pojasni.
[Ovu poruku je menjao Elojd dana 19.01.2006. u 15:09 GMT+1]
[Ovu poruku je menjao Elojd dana 19.01.2006. u 15:23 GMT+1] |
[ Farenhajt @ 19.01.2006. 15:54 ] @
Zamisli da su ti bele numerisane brojevima od

do

, a crne brojevima od
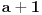
do
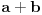
. Sad ti se zadatak svodi na traženje verovatnoće da su izvučena tačno dva broja iz prvog intervala i tačno tri broja iz drugog intervala, a to će očigledno biti
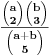
[ Elojd @ 19.01.2006. 18:03 ] @
Hvala na odgovoru, znači ipak se kuglice posmatraju kao da su numerisane iako su iste boje. Nigde ne piše da su kuglice numerisane(a i nisu), pa me je to zbunjivalo. Kao postoji x belih i z crnih.Ja sam to gledao kao da na primer imam skup od recimo X={c,b}
sa mogućnošću ponavljanja.
[Ovu poruku je menjao Elojd dana 19.01.2006. u 19:06 GMT+1]
[ Farenhajt @ 19.01.2006. 18:39 ] @
Tvoj rezon se može primeniti na niz nezavisnih događaja - recimo, na uzastopno bacanje novčića, ili na situaciju kad imamo jednu crnu i jednu belu, pa svaki put vadimo po jednu i beležimo rezultat, a onda izvučenu kuglicu vraćamo u kutiju. Međutim, kada se nekoliko objekata bira jednovremeno, ili ako se objekti vade jedan po jedan bez vraćanja, onda ne možeš primenjivati taj rezon jer događaji nisu nezavisni, već problem moraš nekako svesti na biranje podskupa iz skupa (najčešće to znači pridruživanje numeracije nenumerisanim objektima).
[Ovu poruku je menjao Farenhajt dana 19.01.2006. u 19:40 GMT+1]
[ Elojd @ 19.01.2006. 19:00 ] @
tnx, sad mi je kristalno jasno, ustedeo sam odlazak na konsultacije :)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.