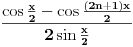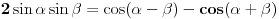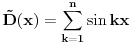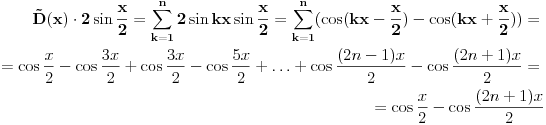[ Kretosh @ 20.01.2006. 18:35 ] @
|
|
sin x + sin 2x+.........sin nx=?
uslovi su da je sin x/2 razlicito od 0 i da je n >= -1
Ja sam koristio neke formule tipa :
sin (x + y)=sin x * cos y + cos x* sin y
pa onda umesto y pisao sin(2x+x) ...sin(3x+x) itd kako bih shvatio algoritam ali
izgleda da je potreban drugaciji pristup. |
[ uranium @ 20.01.2006. 19:51 ] @
ako važi taj uslov, onda je tražena suma jednaka:
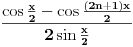
Dokaz.
Koristićemo poznatu činjenicu:
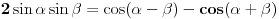
Neka je
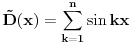
, onda je
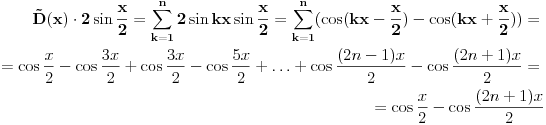
[ Caminero @ 28.01.2006. 21:16 ] @
da li neko moze da mi napise formule (tipa za prvih n prirodnih brojev [n(n+1)]/2 ) za:
2^2 + 4^2 + ... + (2n)^2=..
1^2 + 2^2 + 3^2 + ... + n^2 =
1^2 + 3^2 + 5^2 + ... + (2n+1)^2 =
isto tako i za treci stepen ?!?!?
[ qzqzqz @ 28.01.2006. 23:36 ] @
S [tex]1^2+2^2+...+n^2={n(n+1)(2n+1) \over 6}[\tex]
Ovo se lako dokazuje matematickom induckijom.
Za 1 izvuces 4 ispred svega pa primenjujes ovo gore.............
Za treci(i vece stepene) sume ovog oblika posmatras kao polinom stepena za 1 veceg od stepena sume(exponenta), pa ubacivanjem n=1,2,3,4...... nalazis koeficijente tog polinoma i posle matematickom indukcijom to dokazes.
nadam se da ti je jasno.
[Ovu poruku je menjao qzqzqz dana 29.01.2006. u 00:38 GMT+1]
[ Caminero @ 01.02.2006. 20:03 ] @
hvala,
ako jos samo moze zbir prvih n neparnih brojeva 1+3+5+7+...+(2n+1)
ja sam pokusavao da izvedem iz parnih i prvih n ali mi ne ide...!
(ako uopste postoji...)
[Ovu poruku je menjao Caminero dana 02.02.2006. u 15:53 GMT+1]
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.