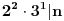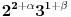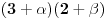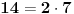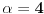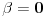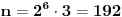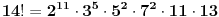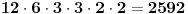[ malada @ 22.01.2006. 07:48 ] @
| Odrediti prirodan broj n koji ima sledeca svojstva: deljiv je sa 3 i sa 4 i ima ukupno 14 razlicitih delilaca. Posto je ovo ispitni zadatak interesuje me dali je jedno od rijesenja 14! ili ima neka, meni strana, fora, jer nema nikakvih restrikcija tipa "najmanji" zadatak glasi bas ovako kako sam ga napisao. |