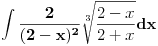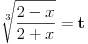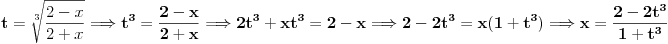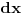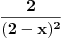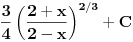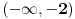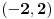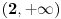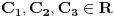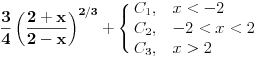[ jelena-dj @ 29.01.2006. 11:47 ] @
| integral (2/ (2-x)^2)*trecikoren iz (2-x)/(2+x) dx ja mislim da ovde treba da bude integral (2/ (2+x)^2)*trecikoren iz (2-x)/(2+x) dx zato sto je imenilac izvoda od potkorene velicine (2+x)^2. Sta kazete? Jesam li u pravu, il mozda postoji nesto sto nisam primetila? |