Odgovor se nalazi u tvom pitanju Za svako epsilon vece od 0 ... ako je za svako epsilon onda je iza dva epsilon i epsilon polovina.

Nisam baš siguran da sam razumeo pitanje, ali...

Ako je 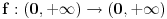surjekcija i ako, primera radi, dokažemo:

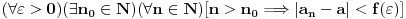
a želeli bi da dokažemo:
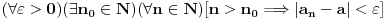
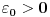
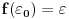
, onda je dovoljno primetiti da za dato uvek postoji , za koje važi pa upotrebiti ono prvo tvrđenje za .

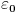
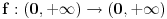
A slično bi prošla i varijanta kada je: i .


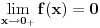
_{[Ovu poruku je menjao uranium dana 01.02.2006. u 13:16 GMT+1]}

Da, evo uranium je to lijepo zapisao. Kod definicije limesa je bit da epsilon moze biti beskonacno mala velicina, uvijek apsolutnu vrijednost razlike |a[n]-a| mozes naciniti po volji malom, tj. manjom od tog epsilona, tako da definicija vrijedi za svako epsilon i za svako epsilon/[bilo koji broj iz R].

_{[Ovu poruku je menjao bierkof dana 10.02.2006. u 20:08 GMT+1]}