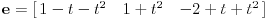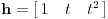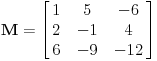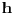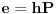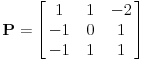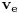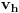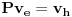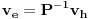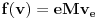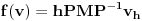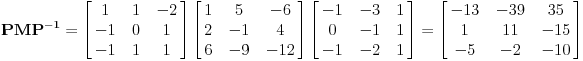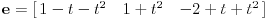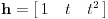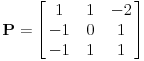[ bunika @ 01.02.2006. 13:39 ] @
| Ovako, imam ispit za nekih 5 dana, a nisam uspio preci zadatke sa linearnim operatorima, pa ako ima neko da se u to konta, zamolio bih ga da mi to objasni. Napisacu jedan primjer, pa da kroz njega prodjemo detaljno. Ispit mi je uskoro pa je odgovor pozeljan sto prije. Zadatak je: Linearan operator f : P2(R) - P2(R) ima u odnosu na bazu {1-t-t(na kvadrat), 1+t(na kvadrat),-2+t+t(na kvadrat)} matricu M = {1 5 -6, 2 -1 4, 6 -9 -12} (brojevi su napisani po vrstama) Odrediti matricu operatora f u odnosu na bazu {1,t,t(na kvadrat)}. Izvinjavam se zbog ovakvog pisanja, ali nisam znao kako da ubacujem matrice, kvadrate i sl. Unaprijed zahvalan. Pozdrav |