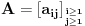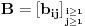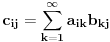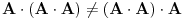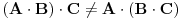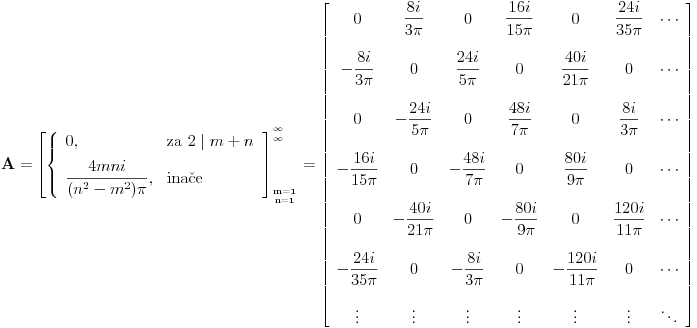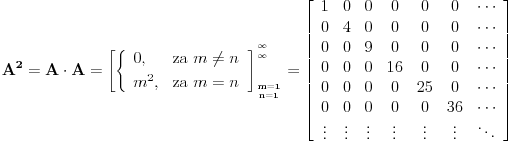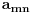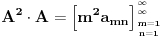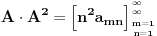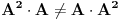[ petarm @ 05.02.2006. 15:01 ] @
| Imam jedno pitanje iz linearne algebre. Naime znamo da je mnozenje matrica asocijativno za konacne matrice. Ali za beskonacne to ne mora da znaci. Cak moze da vazi da je A x (AxA) razlicito od (AxA)xA. Za kvadratnu matricu znamo da moze imati samo jednu inverznu matricu. Odnosno ako pretpostavimo da postoje dve inverzne matrice B i C, matrice A lako uz pomoc jedinicne matrice I i zakona asocijativnosti pokazujemo da je B=C. Ali da li to vazi i za beskonacne matrice? Tu svakako ne mogu koristiti zakon asocijativnosti da bih pokazao da postoji samo jedna inverzna matrica neke beskonacne matrice. Moje pitanje je da li postoji neki drugi nacin za ovaj dokaz ili beskonacne matrice mogu imati vise inverznih matrica? |